Общие правила построения двойственных пар

1. Каждому i - му ограничению исходной задачи соответствует переменная 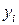и, наоборот, каждому

j-му ограничению двойственной задачи соответствует переменная 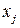исходной задачи.

2. Матрицы А из коэффициентов ограничений прямой и двойственной задач взаимно транспонированы, т.е., строки одной матрицы являются столбцами другой, сохраняя свой порядковый номер.

3. Свободные члены ограничений одной из задач являются коэффициентами при соответствующих переменных в целевой функции другой задачи. При этом максимизация одной функции меняется на минимизацию другой, и наоборот.

4. В исходной задаче ограничения – неравенства следует записывать со знаком « 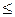» при максимизации и со знаком « 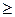» при минимизации.

5. Каждому i-му ограничению- неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности 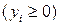, равенству- переменная 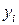без ограничений. Наоборот, неотрицательной переменной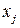 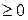соответствует в двойственной задаче- j -е ограничение - неравенство, а произвольной переменной- равенство.

6. Каждой балансовой переменной исходной задачи соответствует основная переменная двойственной задачи и наоборот. При этом число основных переменных одной задачи равняется числу ограничений другой задачи.