Аудиториялық жұмыстар

Берілген дифференциалдық теңдеудің шешімі болатын у функциясын тап, мұндағы С,С₁,С₂ ,С₃ - кез келген тұрақты сандар.

1⁰. .

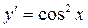A) ;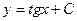

B) ;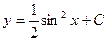

C) ;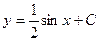

D) ;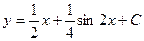

E) ;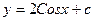

2⁰. .

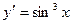A) ;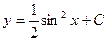

B) ;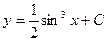

C) ;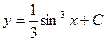

D) ;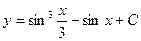

E) ;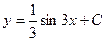

3⁰. .

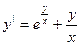A) ;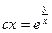

B) ;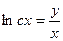

C) ;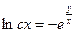

D) ;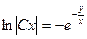

E) ;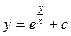

4⁰. .

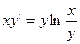A) ;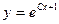

B) ;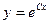

C) ;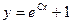

D) ;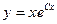

E) ;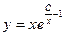

5⁰. .

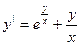A) ;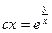

B) ;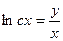

C) ;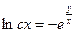

D) ;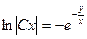

E) ;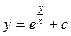

6⁰. .

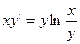A) ;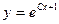

B) ;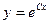

C) ;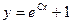

D) ;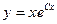

E) ;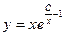

7⁰.

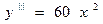
A) ;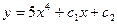

B) ;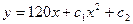

C) ;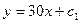

D) ;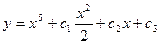

E) ;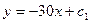

8⁰.

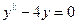
A) ;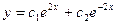

B) ;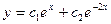

C) ;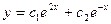

D) ;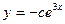

E) ;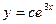

Й жұмыстары

Берілген дифференциалдық теңдеудің шешімі болатынын у функциясын тап, мұндағы С,С₁,С₂ ,С₃ - кез келген тұрақты сандар.

9⁰. .

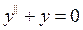A) ;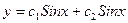

B) ;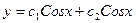

C) ;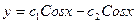

D) ;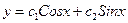

E) ;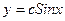

10⁰.

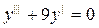
A) ;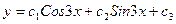

B) ;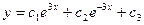

C) ;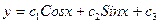

D) ;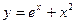

E) ;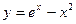

11⁰.

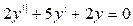
A) ;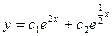

B) ;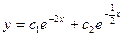

C) ;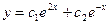

D) ;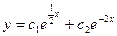

E) ;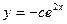

12⁰.

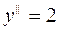
A) ;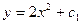

B) ;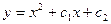

C) ;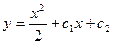

D) ;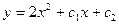

E) ;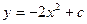

13⁰.

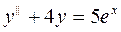
A) ;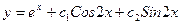

B) ;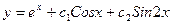

C) ;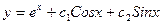

D) ;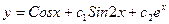

E) ;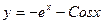

14⁰. y^//+y=0

A)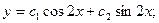

B)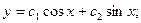

C)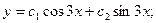

D)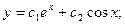

E) ;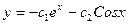

БІРІНШІ РЕТТІ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

Анықтама. Бірінші реттідифференциалдық теңдеу деп 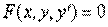түріндегі теңдеуді айтады.

Егер бұл теңдік у^/ арқылы шешілсе, яғни 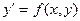түрінде жазылса, онда соңғы теңдеу туындысы арқылы шешілген дифференциалдық теңдеу делінеді.

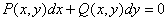- бұл бірінші ретті теңдеудің дифференциалды түрі деп аталады.

Анықтама. Бірінші ретті дифференциалдық теңдеудіңжалпы шешімі деп кез-келген бір тұрақты С–дан тәуелді және келесі шарттарды қанағаттандыратын 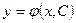функциясын айтады:

а) ол С тұрақтының кез келген мәнінде дифференциалдық теңдеуді қанағаттандырады;

ә) бастапқы шарт х=х₀ болғанда у=у₀ қандай болмаса да 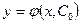функциясы берілген бастапқы шартты қанағаттандыратындай С=С₀ мәнін табуға болады ;

Анықтама. Дифференциалдық теңдеудің 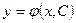жалпы шешіміндегі с тұрақтысына 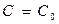мәнін берсеk, онда 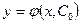- теңдеудің дара шешімі деп аталады.

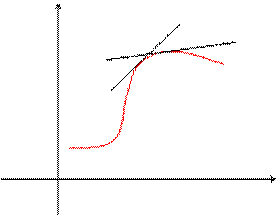
Дифференциалдық теңдеудің шешімі болатын функция арқылы берілген S қисығы 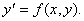теңдеуінің интегралдық қисығы делінеді.

Айнымалылары ажыратылатын теңдеулер

Анықтама. 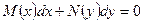- айнымалысы ажыратылған теңдеу, 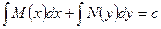- оның жалпы интегралы деп аталады.

Мысалы: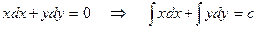

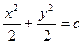
- берілген теңдеудің жалпы интегралы.

Анықтама. 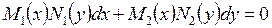- түріндегі теңдеу айнымалысы ажыратылатын теңдеу деп аталады.

Бұл теңдеуді шешу үшін оның екі жағын да 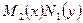көбейтіндісіне бөлеміз. Сөйтіп, айнымалысы ажыратылған теңдеу алуға болады.

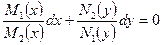
Мысал 1: 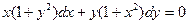теңдеудің интегралын тап:

Шешуі:

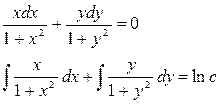
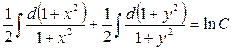
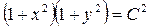- жалпы интеграл.

Мысал 2: 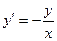дифференциалдық теңдеудің жалпы және дара шешімдерін табайық.

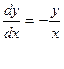
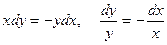
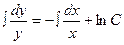
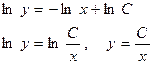
берілген теңдеудің жалпы шешімі. 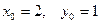болғандағы теңдеудің дара шешімін табатын болсақ: 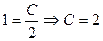. Олай болса, 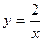берілген теңдеудің дара шешімі.

Аудиториялық жұмыстар

Теңдеу түрін анықтап, жалпы интегралын немесе жалпы шешімін жəне бастапқы шарт берілгендері үшін оны қанағаттандыратын дара шешімін тап.

1⁰. хуу^/=1-x² жауабы: x²+y²=lnCx²

2⁰. 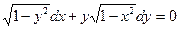жауабы: 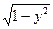=arcsinx+C

3⁰. y^/ tqx-y=a жауабы: y=Csinx-a

4⁰. 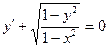жауабы: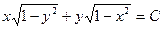

5⁰. xy^/+y=y² жауабы: Cx=(y-1)/y

6⁰. e ^{– s} (1+ds/dt )=1 жауабы: e ^t =C(1-e ^{- s})

7⁰. y^/ =10 ^{x + y} жауабы: 10 ^x +10^-у=C

8⁰. y ^/+sin(x + y)/ 2= sin(x − y)/2 жауабы: ln½ tq y/4½=C −2sin(x/2)

9⁰. 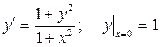жауабы: у=(1+х)/(1-х)

10⁰. 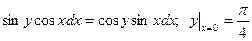жауабы: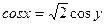

Й жұмыстары

Айнымалылары ажыратылған дифференциалдық теңдеулерге есептер. Теңдеу түрін анықтап, жалпы интегралын немесе жалпы шешімін жəне бастапқы шарт берілгендері үшін оны қанағаттандыратын дара шешімін тап.

11⁰. (х+1)³dx- (у-2)² dx=0;

12⁰. y-xy'=b(1+x²y^'/); yï_х=1= 1

13⁰. sec²xsecydx= -ctgxsinydy

14⁰. y ′ = 2 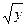ln x , у(е)=1

15⁰. ( 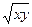+ 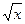) y′ − y = 0

16⁰. xy′ + y = y ², у(1)=1/2

17⁰. 2^x+y +3^x−2y y′ =0

18⁰. (1+e ^x)y⋅ y′ =e^y, у(0)= 0

19⁰. 20xdx-3ydy=3x²ydy-5xy²dx

20⁰. y′сtgх + y = 0, у(0)= -1

21⁰. у'=(1+у²)/( 1+х²)

22⁰. (x² −1)y′ +2xy² = 0, у(0)=1

23⁰. x²y′+ y =0

24⁰. (a² +y²)dx+2x 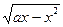dy=0, у(а)=0

25⁰. -ху'=а(1+х²у')

26⁰. (x +2y)y ′ =1, у(0)= -1

26⁰. x + xy + yy′ (1+ x ) = 0

27⁰. (1+e^2x)y²dy−e^xdx=0, у(0)=1

28⁰. sinxsinydx+cosxcosydy=0

29⁰. (1+ x²)y′ + y 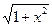= xy, у(0)=1