Среднеквадратичная погрешность среднего арифметического
Пусть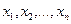 
- результаты отдельных измерений, каждое из которых характеризуется одной и той же дисперсией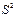 
Найдем выражение для среднего арифметического: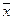 
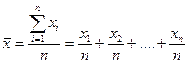
Т.к. дисперсия суммы равна сумме дисперсий слагаемых, то дисперсия величины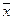
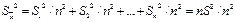
При равноточных измерениях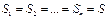 
. Следовательно,
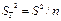и 
.
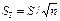Дисперсия среднего арифметического в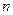 
раз меньше дисперсии отдельного измерения в серии 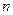измерений. А среднеквадратичная погрешность среднеквадратичного в 
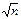раз меньше среднеквадратичного отдельного измерения. Из этого следует важный практический вывод: желая повысить точность измерений в 
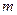раз, нужно увеличить число измерений в 
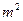раз.
§ 7 Определение коэффициентов линейной зависимости по МНК - вывод.
Пусть в эксперименте измерен ряд значений некоторой величины x и, соответствующие им значения, величины y. Между ними справедлива зависимость вида: y = ax + b.
Тогда сумма квадратов расстояний от экспериментальных точек до прямой будет равна:
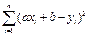
Для решения задачи на нахождение минимума этого выражения необходимо приравнять нулю производные от этой суммы по двум неизвестным величинам a и b.
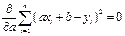
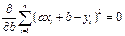
Взяв производные, получаем:
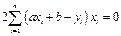
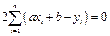
Преобразуем эти уравнения:
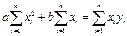
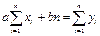
Решение системы из двух уравнений с двумя неизвестными приводит к следующим выражениям для коэффициентов a и b.
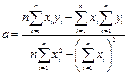
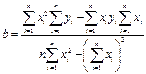
Литература
& Вентцель Е.С. “Курс теории вероятностей“, М.,Наука, 1976, 464с.
& Агекян Т.А. “Теория вероятностей для астрономов и физиков“, М., Наука, 1974, 264с.
& Гольцман Ф.М. “Физический эксперимент и статистические выводы“, Л., изд. ЛГУ, 1982, 190с.
& Гольцман Ф.М. «Вопросы статистической обработки измерений» СПб, Изд. СПбГУ, 2000г.
& О.Б. Васильев, В.И. Елфимов, С.И. Стальнова, Ю.Г. Шишкин. Математическая обработка результатов физического эксперимента // Изд-во Ленинградского университета, Л-д, 1989, 33 с.
& Соловьев В.А., Яхонтова В.Е. Основы измерительной техники. Руководство к лабораторным работам по физике. Учеб. пособие. Л., 1980.
& Соловьев В.А., Яхонтова В.Е. Руководство к лабораторным работам по физике. Учеб. пособие. Изд. С-Петербургского университета, 1997г., 338 с.
& Зайдель А.Н. «Ошибки измерений физических величин», Ленинград, изд. Наука, 1974г., 108 с
& Дж. Сквайрс Практическая физика. М, Мир, 1971г., 246 с.
& Дж. Тейлор Введение в теорию ошибок, М., Мир, 1985 г., 272 с
* Подробнее о способах оценки не исключенной систематической погрешности смотри ниже, главу 6 «Учет погрешности приборов»
* О том, как это следует делать см. ниже, главу «Практические способы расчета случайных погрешностей»
* Это касается только случайных погрешностей. Поскольку всегда присутствуют и погрешности обусловленные точностью измерительных приборов, то проводить очень большое количество измерений не рационально.
* Для нормального распределения среднее значение совпадает с наиболее вероятным, надо отметить, что это справедливо не для любого распределения
* Здесь величины X1,X2,…Xn не разные значения одной и той же физической величины, а разные физические величины.
* Имеется в виду оценка границ доверительного интервала с указанием доверительной вероятности. При других способах оценки чаще оставляют в погрешности только одну цифру.