Пример. Заданы последовательности (начало координат в нижнем левом углу): s(n,m) = , h(n,m) =
Заданы последовательности (начало координат в нижнем левом углу): s(n,m) = 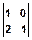 , h(n,m) =
, h(n,m) = 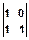 .
.
Вычислить свертку z(n,m) = s(n,m) ** h(n,m).
ДПФ размера 2 х 2 для s(n,m). S(0,0) = s(0,0) + s(1,0) + s(0,1) + s(1,1) = 2+1+1+0 = 4
S(1,0) = s(0,0) - s(1,0) + s(0,1) - s(1,1) = 2 -1+1 -0 = 2
S(0,1) = s(0,0) + s(1,0) - s(0,1) - s(1,1) = 2+1 -1 -0 = 2
S(1,1) = s(0,0) - s(1,0) - s(0,1) + s(1,1) = 2 -1 -1+0 = 0
После аналогичного вычисления H(k,l) и перемножения S(k,l)= S(k,l) H(k,l):
S(k,l) = 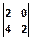 , H(k,l)=
, H(k,l)= 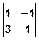 , Z(k,l)=
, Z(k,l)= 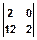 .
.
После обратного ДПФ размера 2 х 2 получим результат циклической свертки: z(n,m) = 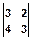 .
.
Дополним опорные области s(.) и h(.) до размера 4 х 4 (для исключения искажения спектра, в принципе,
достаточен размер 3 х 3), и повторим вычисления:
s(n,m)= 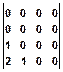 , h(n,m)=
, h(n,m)= 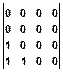 .
.
S(k,l)= 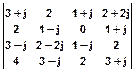 , H(k,l)=
, H(k,l)= 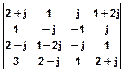 .
.
S(k,l)= 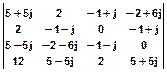 . s(n,m)=
. s(n,m)= 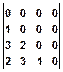 .
.
Сравнение данного результата с ДПФ размером 2 х 2 позволяет наглядно видеть эффект
цикличности свертки.
В настоящее время имеются разнообразные и весьма эффективные алгоритмы ДПФ. Для прямого вычисления P-мерного ДПФ требуется (N1 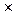 N2
N2 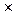 ...
... 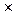 NP)2 операций умножения и сложения. Для многомерного ДПФ, как и для одномерного, существуют алгоритмы быстрых преобразований Фурье. Простейший из них в двумерном ДПФ - разбиение на строки и столбцы, который мы уже рассматривали. Аналогично, Р-мерное ДПФ может заменяться Р-операциями одномерных ДПФ, при этом общее количество операций умножения и сложения сокращается.
NP)2 операций умножения и сложения. Для многомерного ДПФ, как и для одномерного, существуют алгоритмы быстрых преобразований Фурье. Простейший из них в двумерном ДПФ - разбиение на строки и столбцы, который мы уже рассматривали. Аналогично, Р-мерное ДПФ может заменяться Р-операциями одномерных ДПФ, при этом общее количество операций умножения и сложения сокращается.
литература
9. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. – М.: Мир, 1988. – 488 с.
