Прямая и плоскость в пространстве
Учебно-методическое пособие по дисциплине «Высшей математике» для студентов-заочников 1-го курса
Составитель- разработчик: ст. преподаватель Кобяк Г.Ф. Учебно-методическое пособие по дисциплине «Высшей математике» для студентов-заочников 1 курса
Учебно-методическое рекомендовано к изданию решением кафедры математики и информатики.
ОСНОВНЫЕ ФОРМУЛЫ.
Даны два вектора со своими координатами
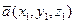 и
и 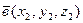
1) тогда скалярное произведение двух векторов:
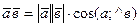 =
= 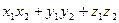
2.) если 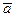 ^
^ 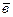 , то
, то 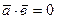 ; 3.) если
; 3.) если 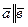 , то
, то 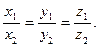
4) Абсолютная величина (модуль) вектора: 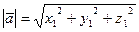
5) Угол между векторами:
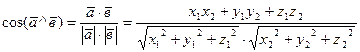
6) Общее уравнение прямой:
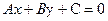
7) Уравнение прямой с угловым коэффициентом имеет вид:
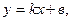 где
где 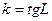 (L угол наклона прямой к оси
(L угол наклона прямой к оси 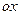 ),
), 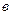 - ордината точки пересечения прямой с осью
- ордината точки пересечения прямой с осью 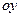 .
.
8) Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом:
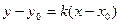 , где
, где 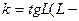 угол, образуемый прямой с осью
угол, образуемый прямой с осью 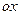 );
);
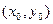 - координаты данной точки.
- координаты данной точки.
9) Уравнение прямой, проходящей через две данные точки 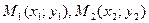 , где
, где 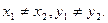
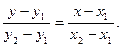
10) Нормальное уравнение прямой:
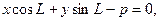
где р – длина перпендикуляра, опущенного из начала координат на прямую, L – угол, который этот перпендикуляр образует с положительным направлением оси 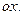
11) Общее уравнение прямой (6) можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель 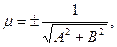 знак выбирается из условия:
знак выбирается из условия: 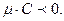
12) Расстояние от точки до прямой: 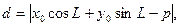 где
где 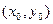 - координаты точки,
- координаты точки, 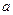
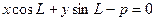 нормальное уравнение прямой.
нормальное уравнение прямой.
13) Угол между двумя прямыми:
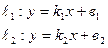
находится по формуле
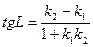
если 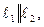 то
то 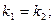 если
если 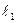 ^
^ 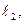 то
то 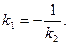
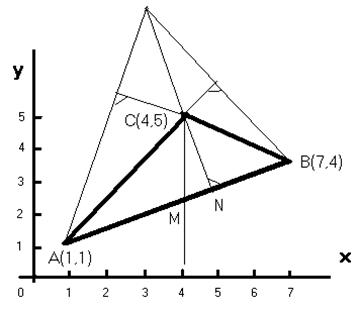
Пример 1.Даны вершины А (1; 1), В (7, 4), С (4, 5) треугольника.
Найти: 1) длину стороны АВ; 2) внутренний угол А; 3) уравнение высоты, опущенной из вершины С; 4) уравнение медианы, проведенной из вершины С; 5) точку пересечения высот треугольника; 6) длину высоты опущенной из вершины С; 7) определить систему линейных неравенств, определяющих внутреннюю область треугольника АВС. Сделать чертеж.
Решение:
1) Длина стороны АВ равна 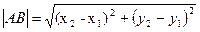 =
= 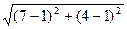 =
= 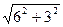 =
= 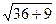 =
= 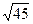 =
= 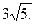
2) Находим угловые коэффициенты прямых АВ и АС:
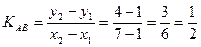
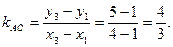
Тогда
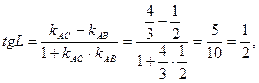
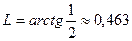 рад.
рад.
3) Пусть высота, опущенная из вершины С, пересечет прямую АВ в точке N. Прямые АВ и СN перпендикуляры, значит их угловые коэффициенты 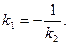
Запишем уравнение прямой АВ: 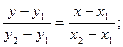
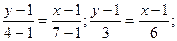
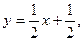
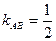 тогда у прямой СN угловой коэффициент будет
тогда у прямой СN угловой коэффициент будет 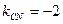
Уравнение высоты СN: 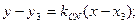
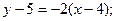
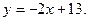
4) Для получения медианы, проходящей через вершину С, находим координаты середины АВ – точки М 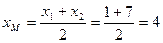
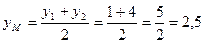 тогда уравнение прямой СМ
тогда уравнение прямой СМ
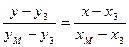 или
или 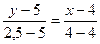
откуда видно, что медиана параллельна оси ОУ и ее уравнение х =4.
5) Находим точку пересечения высот треугольника. Для этого напишем уравнение высоты, проходящей через точку В.
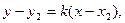
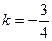
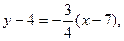
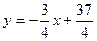
Координаты точки пересечения высот удовлетворяют системе уравнений.
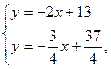 откуда
откуда 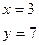
6) Находим длину высоты, опущенной из вершины С. Находим координаты точки пересечения этой высоты со стороной АВ, т.е. решим систему:
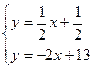
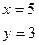
Тогда длина высоты равна 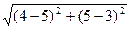 =
= 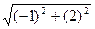 =
= 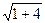 =
= 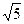
7) Запишем систему линейных неравенств, определяющих внутреннюю область 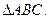 Для этого надо написать уравнение сторон треугольника:
Для этого надо написать уравнение сторон треугольника:
АВ: 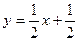 или
или 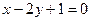
АВ: 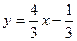 или
или 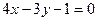
АВ: 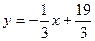 или
или 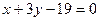
Прямая АВ разбивает плоскость на две полуплоскости. Одна из них определяется неравенством х – 2у + 1 < 0, которому удовлетворяет точка С: 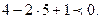
Неравенство 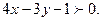 Определяет полуплоскость, содержащую точку В.
Определяет полуплоскость, содержащую точку В.
И наконец, 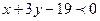 - это полуплоскость, содержащая точку А.
- это полуплоскость, содержащая точку А.
 |
Итак, искомая система неравенств, которая определяет все точки, лежащие внутри треугольника АВС, имеет вид:
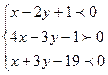
14) Уравнение плоскости, проходящей через точку 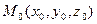 перпендикулярно вектору
перпендикулярно вектору 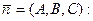
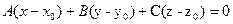
15) Общее уравнение плоскости: 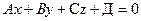
Вектор 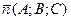 называется нормальным вектором плоскости.
называется нормальным вектором плоскости.
16) Уравнение плоскости в отрезках
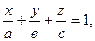 где
где
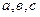 - абсцисса, ордината и аппликата точек пересечения плоскостью координатных осей Ох, Оу и Оz соответственно.
- абсцисса, ордината и аппликата точек пересечения плоскостью координатных осей Ох, Оу и Оz соответственно.
17) Уравнение плоскости, проходящей через три данные точки 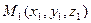 ,
, 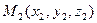 и
и 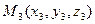 :
:

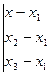
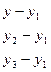
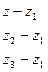 = 0
= 0
Чтобы привести общее уравнение плоскости к нормальному виду надо умножить его на нормирующий множитель 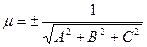 , где знак
, где знак 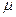 выбирается из условия
выбирается из условия 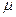
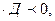 тогда:
тогда: 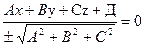 или
или 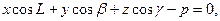 где
где
Р = длина перпендикуляра, опущенного из начала координат на плоскость, 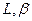 , γ – углы образованные единичным вектором
, γ – углы образованные единичным вектором 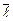 , имеющего направление перпендикуляра, с осями Ох, Оу и Оz.
, имеющего направление перпендикуляра, с осями Ох, Оу и Оz.
18). Расстояние от точки до плоскости находится по формуле 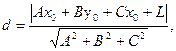 где
где
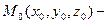 данная точка.
данная точка.
19). Угол между двумя плоскостями:
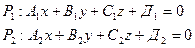 находится по формуле:
находится по формуле:
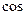 γ =
γ = 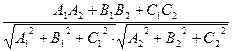
20). Условие параллельностей 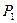 и
и 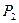 :
:
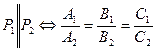
21) Угловые перпендикулярности двух плоскостей 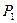 и
и 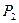 :
:
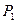 ^
^ 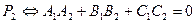
ПРЯМАЯ В ПРОСТРАНСТВЕ
22) Параметрические уравнения в прямой: 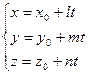
где ( 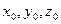 ) – точка, через которую проходит прямая, параллельно вектору
) – точка, через которую проходит прямая, параллельно вектору 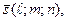
23) t – переменный параметр 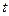 εR. Исключая из уравнений параметр t, получим канонические уравнения прямой:
εR. Исключая из уравнений параметр t, получим канонические уравнения прямой:
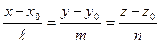
24)Угол между двумя прямыми 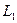 и
и 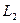 находится по формуле:
находится по формуле:
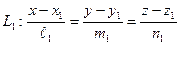
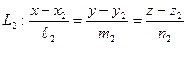
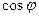 =
= 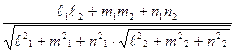
25) Условие параллельности прямых 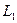 и
и 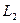 :
:
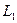 ║
║ 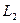 Û
Û 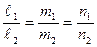
26) Условие перпендикулярности прямых 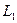 и
и 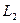 :
:

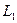 ^
^ 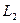 Û
Û 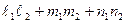 = 0
= 0
Прямая и плоскость в пространстве
27) Угол между прямой 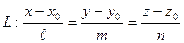 и плоскостью
и плоскостью
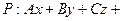 Д = 0 находится по формуле:
Д = 0 находится по формуле: 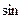
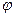 =
= 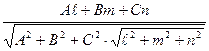
28) Условие параллельности прямой и плоскости: L ║ P Û A 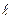 + Bm + Cn = 0
+ Bm + Cn = 0
29) Условие перпендикулярности прямой и плоскости: 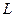 ║ Р Û
║ Р Û 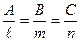

Координаты точки пересечения находятся из системы уравнений
30) 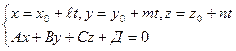
Пример 2.Составить уравнение плоскости, проходящей через точку М (1; -3; -2) параллельно плоскости 3х-2у+4z-3=0
Решение.Ищем уравнение плоскости в виде Ах + Ву + Сz + Д = 0. Две параллельные плоскости имеют общую нормаль 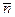 = (3; -2; 4). Следовательно уравнение искомой плоскости имеет вид 3х – 2у + 4z + Д = 0.
= (3; -2; 4). Следовательно уравнение искомой плоскости имеет вид 3х – 2у + 4z + Д = 0.
Точка М (1; -3; -2) по условию лежит в искомой плоскости. Следовательно, подставкой координат 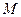 в уравнение плоскости получим тождество:
в уравнение плоскости получим тождество: 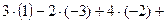 Д = 0.
Д = 0.
Отсюда находим, что Д = - 1. Уравнение искомой плоскости имеет вид 3х-2у+4z-1=0.
Пример 3.Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и удаленной от точки М (3; 4; -2) на расстояние d=5.
Решение.Уравнение искомой плоскости ищем в виде х – 2у + 2z + Д = 0.
Найдем значение Д. Т.к. точка М удалена от искомой плоскости на расстояние d = 5, то по формуле (18) записываем 5 = 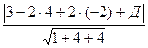 или 5 =
или 5 = 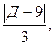 т.е. 15 =
т.е. 15 = 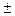 (Д - 9) откуда Д = 24 и Д = -6. Условию задачи удовлетворяют две плоскости: х – 2у + 2z + 24 = 0, и
(Д - 9) откуда Д = 24 и Д = -6. Условию задачи удовлетворяют две плоскости: х – 2у + 2z + 24 = 0, и
Х – 2у + 2z – 6 = 0.
Пример 4.Найти уравнение прямой, проходящей через точку М (-2; 3; 4) и перпендикулярной прямым 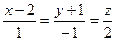 и
и 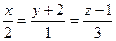
Решение.Уравнение искомой прямой имеет вид 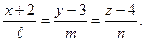 Найдем
Найдем 
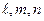 - координаты направляющего вектора
- координаты направляющего вектора 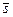 этой прямой. Используя условие перпендикулярности прямых, можно записать:
этой прямой. Используя условие перпендикулярности прямых, можно записать:
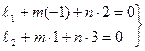
По правилу решения системы двух линейных однородных уравнений с тремя неизвестными находим:





 -1 2 1 2 1 -1
-1 2 1 2 1 -1
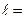 t = -5t, m = - t = t, n = t = 3t, где t – число
t = -5t, m = - t = t, n = t = 3t, где t – число
1 3 2 3 2 1
Уравнение искомой прямой есть 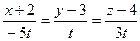 или
или 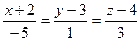
Пример 5.Найти координаты точки, симметричной точке 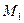 (3; 4; 5) относительно плоскости х – 2у + z - 6 = 0.
(3; 4; 5) относительно плоскости х – 2у + z - 6 = 0.
 Решение.Точка
Решение.Точка 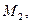 симметричная точке
симметричная точке 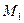 , относительно плоскости, находится на перпендикуляре к плоскости, находится на перпендикуляре к плоскости и является концом отрезка
, относительно плоскости, находится на перпендикуляре к плоскости, находится на перпендикуляре к плоскости и является концом отрезка 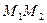 для которого серединой будет точка N пересечения прямой
для которого серединой будет точка N пересечения прямой 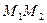 и плоскости. Направляющий вектор перпендикуляра к плоскости – это вектор-нормаль этой плоскости
и плоскости. Направляющий вектор перпендикуляра к плоскости – это вектор-нормаль этой плоскости 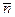 = (1; -2; 1). Уравнение перпендикуляра к плоскости, проведенного через точку
= (1; -2; 1). Уравнение перпендикуляра к плоскости, проведенного через точку 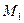 , имеет вид
, имеет вид
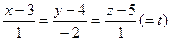 или
или 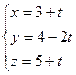 Координаты точки N пересечения перпендикуляра с плоскостью находим, решая систему (30)
Координаты точки N пересечения перпендикуляра с плоскостью находим, решая систему (30) 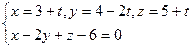
Из равенства 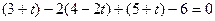 вытекает равенство 6t – 6 =0, т.е. t = 1, следовательно х = 3 + 1 = 4; у = 4 – 2 ´ 1 = 2; z = 5 + 1 = 6, т.е. N (4; 2; 6) – точка пересечения прямой и плоскости. А так как N – середина отрезка М
вытекает равенство 6t – 6 =0, т.е. t = 1, следовательно х = 3 + 1 = 4; у = 4 – 2 ´ 1 = 2; z = 5 + 1 = 6, т.е. N (4; 2; 6) – точка пересечения прямой и плоскости. А так как N – середина отрезка М  M
M 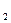 , то
, то
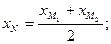
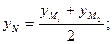
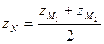
Имеем
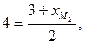
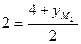 ,
, 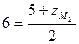
Отсюда находим 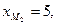
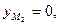
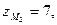 т.е. точка
т.е. точка 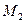 имеет координаты (5; 0; 7).
имеет координаты (5; 0; 7).
Матрицы и определители
Пример 6.Вычислить определять матрицы, разлагая его в сумму по элементам первой строки:
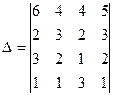
Решение.
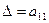
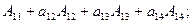
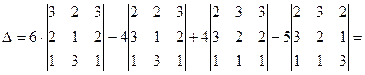
= 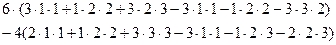
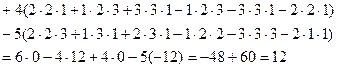
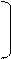
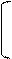 Пример 7.Дана матрица А. Выяснить является ли она невырожденной. Найти матрицу
Пример 7.Дана матрица А. Выяснить является ли она невырожденной. Найти матрицу 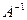 , обратную к А.
, обратную к А.
Решение.1 4 0
А = 1 3 1
-2 4 0
1. Находим определить матрицы А:

 1 4 0
1 4 0
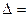 1 3 1 =
1 3 1 = 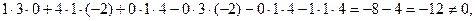
-2 4 0
Значит матрица невыраженная и у нее существует обратная матрица А.
2. Находим алгебраические дополнения для каждого элемента матрицы А.





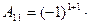 3 1 = - 4,
3 1 = - 4, 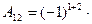 1 1 = -2
1 1 = -2
4 0 -2 0




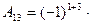 1 3 = 10,
1 3 = 10, 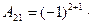 4 0 = 0
4 0 = 0
-2 4 4 0




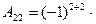 1 0 = 0,
1 0 = 0, 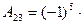 1 4 = -12
1 4 = -12
-2 0 -2 4
 |  |  |  |
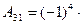 4 0 = 4,
4 0 = 4, 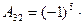 1 0 = -1
1 0 = -1
3 1 1 1


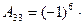 1 4 = -1
1 4 = -1
1 3
3. 
 Составим матрицу
Составим матрицу 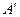 из алгебраических дополнений, взятых в том же порядке, что и элементы матрицы А.
из алгебраических дополнений, взятых в том же порядке, что и элементы матрицы А.
-4 -2 10
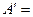 0 0 -12
0 0 -12
4 -1 -1
4. 
 Транспонируем матрицу
Транспонируем матрицу 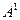 , т.е. поменяем ролями строки и столбцы, получим матрицу
, т.е. поменяем ролями строки и столбцы, получим матрицу 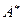 :
:
- 4 0 4
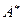 = -2 0 -1
= -2 0 -1
10 -12 -1
5. Разделим каждый элемент матрицы 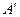 на определитель. Получим обратную матрицу
на определитель. Получим обратную матрицу 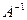 .
.
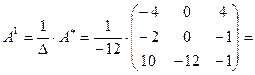
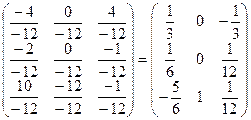



 Проверка:
Проверка: 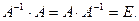

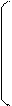 1 4 0
1 4 0 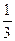 0
0 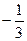 1 0 0
1 0 0
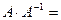 1 3 1
1 3 1 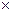
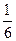 0
0 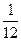 = 0 1 0 = E
= 0 1 0 = E
-2 4 0 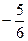 1
1 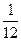 0 0 1
0 0 1
