Механическая система. Силы внешние и внутренние

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - 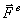, а внутренние - .

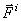Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Внутренние силы обладают следующими свойствами:

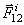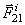1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами и , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

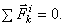
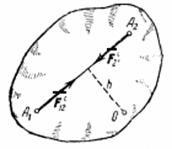
Рис.31

2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.18 видно, что 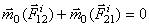. Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет:

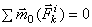или .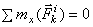

Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело.

Масса системы. Центр масс

Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему

.

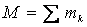В однородном поле тяжести, для которого 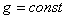, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:

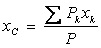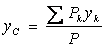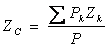, , . (1)

В полученные равенства входят только массы 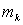материальных точек (частиц), образующих тело, и координаты 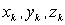этих точек. Следовательно, положение точки С (x_C, y_C, z_C) действительно харак­теризует распределение масс в теле или в любой механической си­стеме, если под 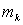, 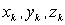понимать соответственно массы и координаты точек этой системы.

Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.

Положение центра масс определяется его радиус-вектором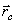

,

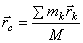где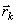 -радиус-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тя­жести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тя­жести, по существу имеет смысл только для твердого тела, находя­щегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная си­стема под действием каких-нибудь сил или нет.