Выравнивании динамических рядов

Вид уравнения	Системы уравнений
Обычный способ рас- чета параметров	Упрощенный способ расчета параметров
Прямая: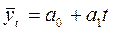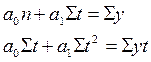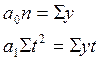
Парабола второго порядка: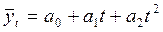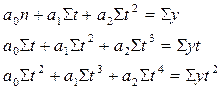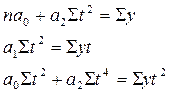
Показательная кри-вая: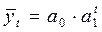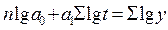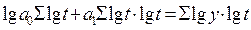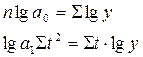
Гипербола: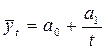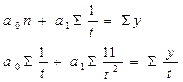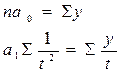

При анализе рядов динамики в ряде случаев возникает необходимость в выявлении сезонных колебаний. Для определения сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет (в основном не менее 3-х лет). При выявлении и оценке сезонности рассчитывают специальные показатели – индексы сезонности ( 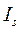). Способы определения индексов сезонности различны и зависят от характера ряда динамики.

В рядах, не имеющих ярко выраженной тенденции развития (или она не наблюдается совсем), изучение сезонности основано на методе простой средней.Сущность этого метода заключается в том, что показатели сезонной волны определяются процентным отношением соответствующих средних месячных (квартальных уровней) к их общей средней за весь изучаемый период. Следовательно, при изучении помесячной сезонности сначала средние по месяцам и среднюю годовую исчисляют из данных за несколько лет (по простой арифметической), а затем эти средние по месяцам года ( 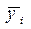)относят к средней годовой (к среднему месячному уровню для взятых лет) ( 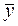), т.е. индекс сезонности исчисляется по формуле:

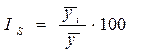
В рядах динамики, имеющих тенденцию развития, для определе-ния индексов сезонности вначале рассчитывают уровни, сглаженные методом скользящей средней или выравненные по определенной функции. Индексы сезонности вычисляются отношением фактического уровня за определенный квартал или месяц ( 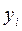) к выравненному за этот же период ( 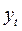). В результате при использовании, например, квар-тальных данных за три года получают двенадцать индексов сезонности:

.

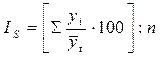Затем исчисляют средние индексы сезонности для одноименных кварталов за рассматриваемые годы:

.

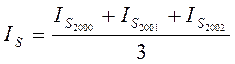В качестве аналитической формы сезонной волны иногда применяется уравнение следующего вида:

,

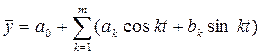где k - порядок гармоники тригонометрического многочлена; t - время; 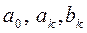- параметры ряда Фурье.

Это уравнение представляет собой ряд Фурье, где время (t) выражается в радиальной мере или в градусах:

Месяцы t

Радиальная мера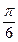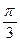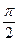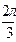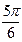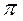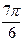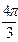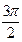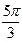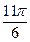

Градусы

Уровни, уi

у1

у2

у3

у4

у5

у6

у7

у8

у9

у10

у11

у12

Обычно при выравнивании по ряду Фурье рассчитывают не более четырех гармоник и затем уже определяют, с каким числом гармоник наилучшим образом отражается периодичность изменения уровней ряда.

Например, при k = 1 уравнение ряда Фурье будет иметь вид:

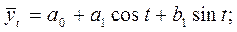
при k = 2 соответственно: .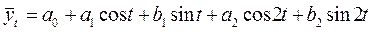

Параметры уравнения находят по способу наименьших квадратов. При этом формулы, используемые для исчисления указанных выше параметров уравнения ряда Фурье имеют вид:

; ; .

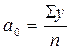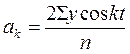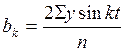Тесты