Погрешность, обусловленная взаимодействием СИТ с объектом на его входе и выходе

Эту погрешность будем исследовать на примере измерительного преобразователя напряжения, подключенного по входу к источнику 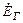с внутренним комплексным сопротивлением 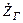и нагруженным на сопротивлении нагрузки 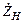. Сам ИП имеет входное сопротивление 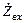, а выходное - .

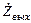В этом случае значение напряжения на входе ИП будет равно

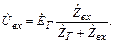(4.49)

Абсолютная погрешность измерения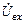

,

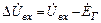а относительная

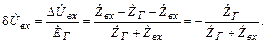(4.50)

Из этого выражения легко получить амплитудную погрешность

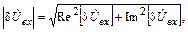
и фазовую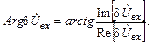

Для чисто активных сопротивлений (на постоянном токе), имеем

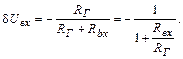(4.51)

Обычно 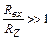, поэтому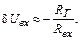

В выходной цепи можно записать аналогичные выражения путем замены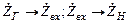

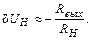(4.52)

Для СИТ неэлектрических величин выражения для погрешности аналогичны, с учетом замены входящих в них параметров на соответствующие неэлектрические.

Контрольные вопросы, задачи и упражнения

1. Что такое СИТ и как они различаются в зависимости от структурной схемы?

2. Чем отличаются СИТ в зависимости от роли, выполняемой ими в процессе измерений?

3. Перечислите классификацию СИТ в зависимости от роли, выполняемой ими в системе обеспечения единства измерений.

4. Перечислите основные принципы нормирования метрологических характеристик.

5. Перечислите основные группы нормируемых метрологических характеристик.

6. Что такое статическая характеристика преобразований, чувствительность и цена деления СИТ?

7. Чем отличаются абсолютная, относительная и приведенная погрешности?

8. Как определить погрешность измерения по классу точности СИТ?

9. Перечислите основные влияющие величины и дайте определение функции влияния.

10. Чем отличаются полные и частные динамические характеристики СИТ?

11. Дайте классификацию полных динамических характеристик.

12. В чем заключается методика аналитического определения динамических характеристик?

13. Какие операции включает в себя методика экспериментального определения динамических характеристик?

14. Как взаимодействие СИТ с объектом измерения влияет на результат измерения?

15. Приведите пример неинформативных параметров выходного сигнала СИТ.

16. Дайте классификацию основным методам измерения.

17. Выведите выражения для относительной погрешности измерения выходной величины СИТ прямого преобразования, обусловленной нестабильностью коэффициентов преобразования его звеньев.

18. Изобразите структурную схему СИТ уравновешивающего преобразования и выведите выражения для его коэффициента преобразования в режимах неполного и полного уравновешивания.

19. Выведите выражения для относительной погрешности измерения СИТ с неполным уравновешиванием, обусловленной нестабильностью коэффициентов прямого и обратного преобразования.

Приложение А

Статистические таблицы

Таблица А.1 – Функция Лапласа

F(z)	z	F(z)	z
0,01	0,0250	0,26	0,7033
0,02	0,0500	0,27	0,7356
0,03	0,0750	0,28	0,7688
0,04	0,1001	0,29	0,8028
0,05	0,1252	0,30
0,06	0,1504	0,31	0,8739
0,07	0,1757	0,32	0,9111
0,08	0,2011	0,33	0,9496
0,09	0,2267	0,34	0,9896
0,10	0,2524	0,35	1,0313
0,11	0,2782	0,36	1,0748
0,12	0,3043	0,37	1,1205
0,13	0,3306	0,38	1,1687
0,14	0,3570	0,39	1,2197
0,15	0,3883	0,40	1,2741
0,16	0,4108	0,41	1,3327
0,17	0,4381	0,42	1,3961
0,18	0,4658	0,43	1,4658
0,19	0,4938	0,44	1,5434
0,20	0,5223	0,45	1,6316
0,21	0,5511	0,46	1,7348
0,22	0,5804	0,47	1,8606
0,23	0,6102	0,48	2,0255
0,24	0,6408	0,49	2,320
0,25	0,6716	0,50	¥

Таблица А.2 – Зависимость вероятности P₀ от l в критерии Колмогорова

P0	1.000	1.000	1.000	1.000	0.997	0.964	0.864
l	0.0	0.1	0.2	0.3	0.4	0.5	0.6

Таблица А.3 – Значения 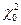для различных K и P₀ в критерии Пирсона

K	Заданная вероятность P0
0.90	0.95	0.99	0.999
	6,215	7,815	11,345	16,27
	7,779	9,489	13,277	18,46
	9,236	11,070	15,086	20,50
	10,645	12,592	16,812	22,50
	12,016	14,067	19,475	24,30

Таблица А.4 – Статистика величины d в составном критерии

n	P = 0,9	P = 0,95	P = 0,99
dmin	dmax	dmin	dmax	dmin	dmax
	0,7409	0,8899	0,7153	0,9073	0,6675	0,9359
0,7452	0,8733	0,7263	0,8884	0,6829	0,9137
0,7495	0,8631	0,7304	0,8768	0,6950	0,9001
0,7530	0,8570	0,7360	0,8686	0,7040	0,8901
0,7559	0,8511	0,7404	0,8625	0,7110	0,6827
0,7583	0,8468	0,7440	0,8578	0,7167	0,8769
0,7604	0,8436	0,7470	0,8540	0,7216	0,8722
0,7621	0,8409	0,7496	0,8508	0,7256	0,8682
0,7636	0,8385	0,7518	0,8481	0,7291	0,8648

Таблица А.5 – Коэффициент распределения Стьюдента для числа измерений n

n	Доверительная вероятность P
0,9	0,95	0,99	0,999
	6,31	12,71	63,68	636,62
	2,92	4,30	9,93	31,60
	2,35	3,18	5,84	12,92
	2,13	2,78	4,60	8,61
	2,02	2,57	4,06	6,87
	1,94	2,45	3,71	5,96
	1,90	2,37	3,50	5,41
	1,86	2,31	3,36	5,04
	1,83	2,26	3,25	4,78
	1,81	2,23	3,17	4,59
	1,80	2,20	3,11	4,44
	1,78	2,18	3,06	4,32
	1,77	2,16	3,01	4,22
	1,76	2,15	2,98	4,14
	1,75	2,13	2,95	4,07
	1,75	2,12	2,92	4,02
	1,74	2,11	2,90	3,97
	1,73	2,10	2,88	3,92
	1,73	2,09	2,86	3,88
	1,65	1,96	2,58	3,29

Таблица А.6 – Зависимость 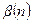в критерии Смирнова

n		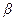n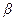
0,9	0,95	0,9	0,95
	1,412	1,414		2,683	2,843
	1,869	1,917		2,718	2,880
	2,093	2,182		2,749	2,913
	2,238	2,349		2,778	2,944
	2,343	2,470		2,805	2,972
	2,426	2,563		2,830	2,998
	2,532	2,670		2,853	3,022
	2,551	2,701		2,874	3,044
	2,601	2,754		2,894	3,065
	2,644	2,801		2,913	3,084

Таблица А.7 – Значения (I–P) –процентных точек распределения Фишера

К2	Р	К1
									¥
	0,9 0,95 0,99	4,11 6,39 16,0	3,94 6,00 14,7	3,88 5,87 14,2	3,84 5,81 14,0	3,83 5,77 13,9	3,82 5,75 13,9	3,80 5,72 13,8	3,79 5,70 13,7	3,78 5,66 13,6	3,76 5,63 13,5
	0,9 0,95 0,99	2,69 4,26 8,02	2,44 3,18 5,35	2,35 3,02 5,00	2,31 2,95 4,84	2,28 2,90 4,73	2,26 2,87 4,66	2,23 2,83 4,57	2,22 2,80 4,52	2,19 2,76 4,42	2,16 2,71 4,31
	0,9 0,95 0,99	2,39 3,11 5,56	2,12 2,65 4,03	2,02 2,48 3,70	1,97 2,40 3,54	1,94 2,35 3,43	1,92 2,31 3,36	1,89 2,27 3,27	1,87 2,24 3,22	1,83 2,19 3,11	1,80 2,13 3,00
	0,9 0,95 0,99	2,27 2,90 4,50	1,98 2,42 3,53	1,88 2,26 3,19	1,82 2,17 3,03	1,79 2,11 2,93	1,76 2,08 2,86	1,73 2,03 2,77	1,71 2,00 2,71	1,67 1,94 2,60	1,63 1,88 2,49
	0,9 0,95 0,99	2,19 2,78 4,22	1,91 2,30 3,26	1,80 2,13 2,93	1,74 2,05 2,77	1,70 1,98 2,66	1,68 1,95 2,59	1,64 1,90 2,50	1,62 1,86 2,44	1,58 1,80 2,33	1,53 1,73 2,21
	0,9 0,95 0,99	2,15 2,70 4,04	1,86 2,22 3,09	1,75 2,05 2,77	1,69 1,96 2,60	1,65 1,90 2,49	1,62 1,86 2,43	1,59 1,81 2,33	1,56 1,78 2,28	1,52 1,71 2,16	1,47 1,64 2,03
	0,9 0,95 0,99	2,10 2,61 3,83	1,79 2,13 2,89	1,68 1,95 2,57	1,62 1,86 2,41	1,58 1,79 2,29	1,55 1,76 2,22	1,52 1,70 2,14	1,49 1,67 2,08	1,44 1,60 1,95	1,39 1,52 1,82
	0,9 0,95 0,99	2,09 2,56 3,73	1,74 2,07 2,79	1,68 1,90 2,47	1,58 1,78 2,28	1,52 1,74 2,19	1,49 1,66 2,11	1,46 1,64 2,02	1,45 1,61 1,96	1,40 1,54 1,85	1,34 1,40 1,62
	0,9 0,95 0,99	2,00 2,46 3,51	1,70 1,97 2,59	1,58 1,79 2,26	1,51 1,60 2,10	1,47 1,63 1,98	1,44 1,59 1,93	1,39 1,50 1,80	1,37 1,49 1,74	1,30 1,39 1,59	1,22 1,28 1,43
0¥	0,9 0,95 0,99	1,94 2,37 3,32	1,63 1,88 2,41	1,51 1,69 2,07	1,43 1,59 1,91	1,38 1,52 1,79	1,35 1,47 1,72	1,30 1,40 1,60	1,26 1,35 1,53	1,18 1,24 1,36	1,00 1,00 1,00

Приложение Б