Алгоритм решения уравнения в полных дифференциалах 5 страница
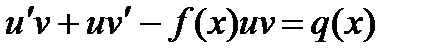
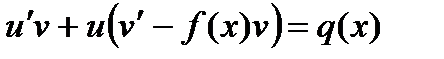
Так как один множитель можно выбрать произвольно, то выберем в качестве v какой-либо частный интеграл уравнения v'—v f(x) = 0 при С = 0.
Подставляя значение v во второе уравнение и решая его, найдем u, как общий интеграл этого уравнения.
Дифференциальные уравнения в полных дифференциалах.
Определение. Дифференциальное уравнение вида 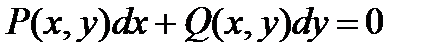 называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение 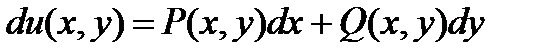 .
.
Общее решение уравнения в полных дифференциалах определяется формулой u(x,y)=C,
где C − произвольная постоянная.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство: ∂Q∂x = ∂P∂y.
Алгоритм решения уравнения в полных дифференциалах
- Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах: ∂Q∂x=∂P∂y.
- Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
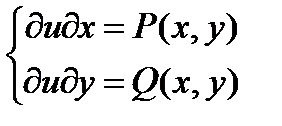 .
. - Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
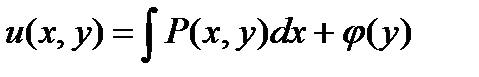 .
. - Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
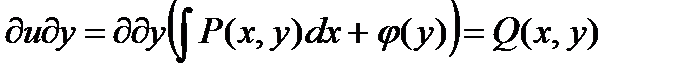 .
.
Отсюда получаем выражение для производной неизвестной функции φ(y):
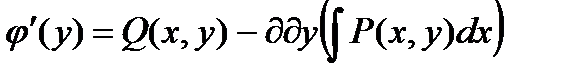 .
.
- Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
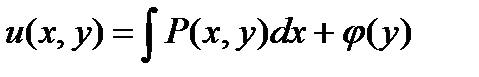 .
.
- Общее решение уравнения в полных дифференциалах записывается в виде:
u(x,y)=C.
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ(x).
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
Найти общее решение уравнения:
1) 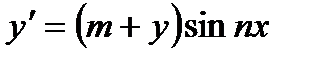 ;
;
2) 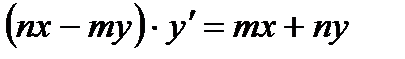 ;
;
3) 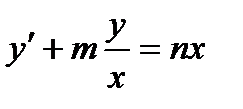 ;
;
4) 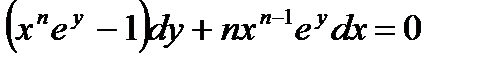 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дифференциальные уравнения. Их виды, порядок, общее и частное решения дифференциальных уравнений.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными.
3. Однородные дифференциальные уравнения и к ним приводящиеся.
4. Дифференциальные уравнения в полных дифференциалах.
5. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.
6.
7.
Практическая работа №15
Тема: Решение дифференциальных уравнений второго порядка.
Цель: Научиться решать дифференциальные уравнения второго порядка.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Дифференциальные уравнения второго порядка.
Если дифференциальное уравнение содержит производную или дифференциал не выше второго порядка, то оно называется дифференциальным уравнением второго порядка.
Общий вид такого уравнения 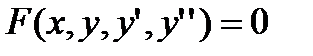 ,
,
где у=f(х)—искомая неизвестная функция, у'=f'(х) и у"=f”(х)—ее производные по х первого и второго порядков, а F — заданная функция переменных х, у, у', y".
Общим решением дифференциального уравнения второго порядка называется функция y=φ(x, C1, C2) от х и двух произвольных постоянных С1 и С2, обращающая это уравнение в тождество по х.
Общее решение, записанное в неявном виде Ф(х, у, С1 С2) =0, называется общим интегралом.
Частным решением уравнения F(х, у, у', у")=0 называется решение, полученное из общего решения при фиксированном значении С1 и С2: у=φ(х, С10, С20 ), где С10 и С20 — фиксированные числа.
Частным интегралом этого уравнения называется интеграл, полученный из общего интеграла при фиксированном значении С1 и С2: Ф(х, у, С10, С20)=0, где С10 и С20 — фиксированные числа.
Общее решение дифференциального уравнения F(х, y, у', у")=0 можно рассматривать как семейство интегральных кривых данного уравнения, зависящее от двух параметров С1 и С2. Частному решению, полученному из общего, соответствует одна кривая этого семейства.
Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти решение, удовлетворяющее начальным условиям у(хо)=у0, у'(хо)=у'0. Постоянные С1 и С2 определяются из системы уравнений
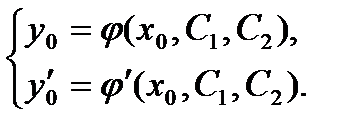
Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить интегральную кривую, проходящую через данную точку (х0, у0) в заданном направлении у'(x0).
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
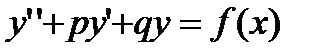 .
.
где р и q — некоторые числа.
Если f(х)= 0, то дифференциальное уравнение называется линейным однородным. Оно имеет вид
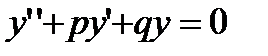 (2)
(2)
Справедлива теорема: если у1 и у2 – частные решения уравнения (2), причем у1/у2 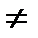 const то функция Y=С1у1+С2y2, где С1 и С2 – произвольные постоянные, является общим решением этого уравнения.
const то функция Y=С1у1+С2y2, где С1 и С2 – произвольные постоянные, является общим решением этого уравнения.
Решением данного дифференциального уравнения (2) должна быть такая функция, которая, будучи подставлена в уравнение, превратит его в тождество. Левая часть уравнения представляет собой сумму функции у и ее производных у' и у", взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма обратилась в нуль, надо, чтобы y, у' и у" были подобны между собой.
Такой функцией является функция у = еkx, где k – постоянная. Требуется подобрать k так, чтобы эта функция удовлетворяла уравнению (2).
Так как у' = еkx (kх)' = k еkx , а y" =k еkx (kx:)'=k2 еkx , то, подставляя эти значения у, у' и у" в левую часть уравнения (2), получим
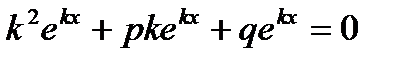 .
.
Сокращая на множитель еkx, не обращающийся в нуль, получим характеристическое уравнение
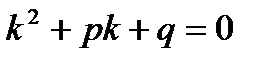 (3)
(3)
Это уравнение определяет те значения А, при которых функция у = еkx является решением дифференциального уравнения (2).
При решении характеристического уравнения (3) возможны три случая:
| № | Корни уравнения | Частные решения | Общее решение |
Действительные различные (k1 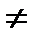 k2) k2) | Y1=ek1x Y2=ek2x | Y=C1ek1x+C2 ek2x | |
| Действительные равные (k1=k2) | Y1=ek1x Y2=xek1x | Y=ek1x(C1+C2x) | |
Комплексно-сопряженные ( 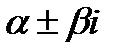 ) ) | Y1=eaxcos 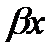 , Y2=eaxsin , Y2=eaxsin 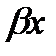  | Y=eax(cos 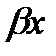 +C2 sin +C2 sin 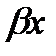 ) ) |
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Решить задачу Коши:
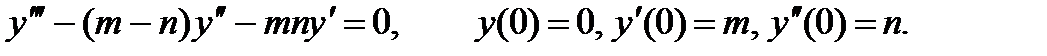
2. Решить уравнение:
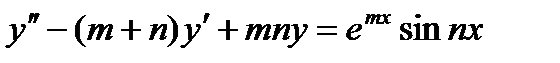 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дифференциальные уравнения высших порядков.
2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
3. Поиск неоднородного решения методами вариации постоянных и неопределенных коэффициентов.
4. Задача Коши.
5.
Практическая работа №16
Тема: Исследование рядов на сходимость.
Цель: Научиться исследовать численные ряды на сходимость используя разные признаки.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Числовой ряд – это сумма членов числовой последовательности вида
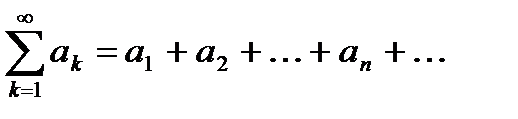 ,
,
где 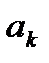 называют общим членом числового ряда или k–ым членом ряда.
называют общим членом числового ряда или k–ым членом ряда.
Определение. Частичная сумма числового ряда – это сумма вида 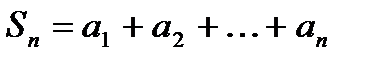 , где n – некоторое натуральное число.
, где n – некоторое натуральное число. 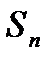 называют также n-ой частичной суммой числового ряда.
называют также n-ой частичной суммой числового ряда.
Определение. Числовой ряд 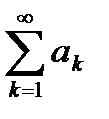 называется сходящимся, если существует конечный предел последовательности частичных сумм
называется сходящимся, если существует конечный предел последовательности частичных сумм 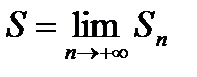 . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд 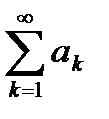 называется расходящимся.
называется расходящимся.
Приведенных определений достаточно для обоснования следующих очень часто используемых утверждений, рекомендуем их запомнить.
1. Гармонический ряд 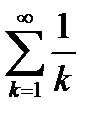 является расходящимся.
является расходящимся.
2. Сумма геометрической прогрессии вида 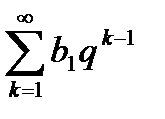 со знаменателем q является сходящимся числовым рядом, если
со знаменателем q является сходящимся числовым рядом, если 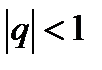 , и расходящимся рядом при
, и расходящимся рядом при 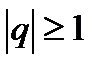 .
.
3. Обобщенно гармонический ряд 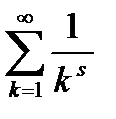 сходится при s > 1 и расходится при s ≤ 1.
сходится при s > 1 и расходится при s ≤ 1.
Определение. Числовой ряд 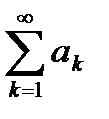 называется знакоположительным, если все его члены положительны, то есть,
называется знакоположительным, если все его члены положительны, то есть, 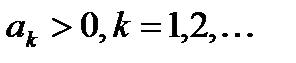 .
.
Определение. Числовой ряд 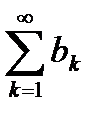 называется знакочередующимся, если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде
называется знакочередующимся, если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде 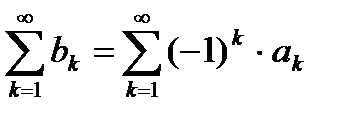 или
или 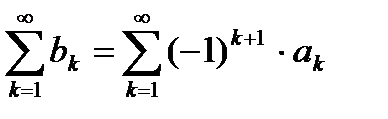 , где
, где 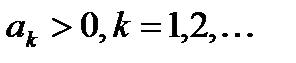 .
.
Определение. Числовой ряд 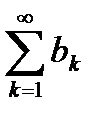 называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов.
называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов.
Для знакопеременного ряда существует понятие абсолютной и условной сходимости.
Определение. Знакопеременный ряд 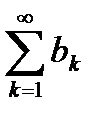 называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд
называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд 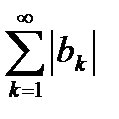 .
.
Определение. Знакопеременный ряд 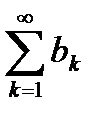 называется условно сходящимся, если ряд
называется условно сходящимся, если ряд 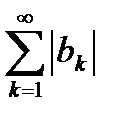 расходится, а ряд
расходится, а ряд 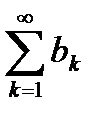 сходится.
сходится.
Свойства сходящихся числовых рядов.
1. Если сходится числовой ряд 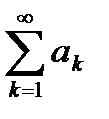 , то сходящимся будет и ряд
, то сходящимся будет и ряд 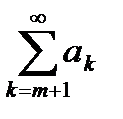 . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду
. Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду 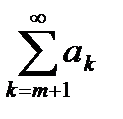 добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
2. Если сходится числовой ряд 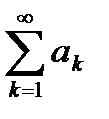 и его сумма равна S, то сходящимся будет и ряд
и его сумма равна S, то сходящимся будет и ряд 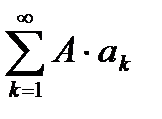 , причем
, причем 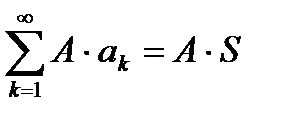 , где A – произвольная постоянная.
, где A – произвольная постоянная.
3. Если сходятся числовые ряды 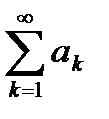 и
и 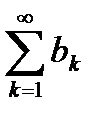 , их суммы равны A и B соответственно, то сходящимися будут ряды
, их суммы равны A и B соответственно, то сходящимися будут ряды 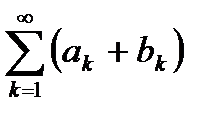 и
и 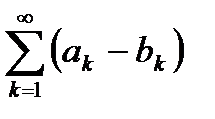 , причем их суммы будут равны A + B и A - B соответственно.
, причем их суммы будут равны A + B и A - B соответственно.
Необходимое условие сходимости ряда.
Если числовой ряд 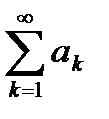 сходится, то предел его k-ого члена равен нулю:
сходится, то предел его k-ого члена равен нулю: 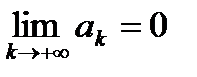 .
.
При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если 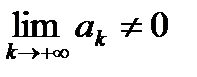 , то ряд расходится.
, то ряд расходится.
Достаточные признаки сходимости знакоположительного ряда.
