Свойство операции вычисления ковариационной матрицы случайного вектора

Если же обобщить свойство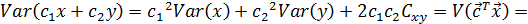

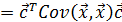на аффинное преобразование случайного вектора 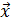в случайный вектор .

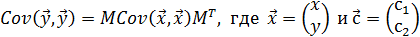14. Случайный вектор и факторизация его ковариационной матрицы. Случайный вектор 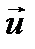случайных остатков в схеме Гаусса – Маркова при гетероскедастичном неавтокоррелированном остатке.

Обратимся к вектору из опыта с бросанием кости. Образуем из его компонент следующие 2 случайных переменных:

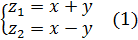
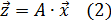
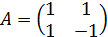
Рассматривая запись, видим, что случайный вектор 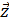является результатом преобразования (1) случайного вектора .

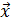Преобразования служат примером аффинного преобразования 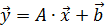(3) случайного вектора 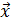в случайный вектор .

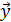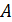- матрица коэффициентов, 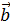- вектор констант.

Отметим правила, по которым можно рассчитать основные количественные характеристики выхода аффинного преобразования:

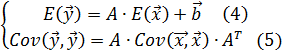
Если 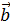=0, то преобразование называется линейным.

Основные характеристики выхода 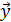рассчитываются по формулам:

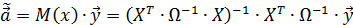
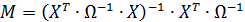
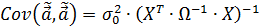
15. Временной ряд и его структура (На примере ВВП России).

Экономическая переменная (пусть ВВП страны), датированная дискретными моментами времени, называется временным или динамическим рядом.

В следующей табличке представлены уровни ВВП страны, выраженные в млрд. руб. в ценах 2000-ого года.

год	1 квартал	2 квартал	3 квартал	4 квартал

Замечание: временные ряды будем обозначать 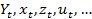Значение переменное времени t будет либо календарными датами (например 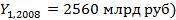, либо эти значения удобно выбрать в виде натуральных чисел.

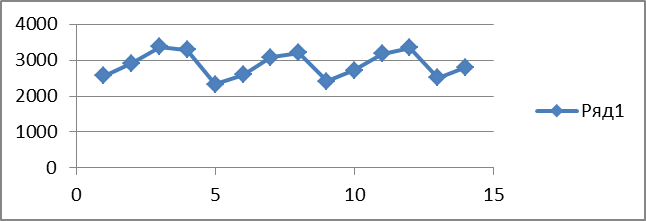
Рассмотрим этот график и сделаем вывод:

В структуре нашего ряда отчетливо видна восходящая тенденция T(t) также видна сезонная составляющая S(t).

Рассматривая график в крупном масштабе, можем обнаружить хаотичное изменение геометрии графика на годичных промежутка времени. Эти изменения порождены присутствием в структуре нашего ряда случайной составляющей .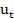

Данные выводы позволяют предложить две основные модели временного ряда:

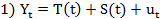- аддитивная модель временного ряда

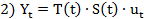- мультипликативная модель

Чтобы составить модель, нужно выбрать модель тренда (некую гладкую непрерывную функцию переменной t) и сезонную составляющую(некую периодическую функцию переменной t с периодом 4 квартала (1 год))

Итог: В общем случае в структуре временного ряда можно выделить три составляющих:

1) Тренд (тенденция);

2) Сезонная составляющая;

3) Случайная составляющая.

________

Временной ряд – это датированная целочисленными моментами времени t экономическая переменная 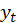. Модели временного ряда предназначены для объяснения (прогноза) уровня ряда 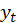фактором времени t.

Изменение переменной 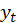определяется следующими тремя факторами:
1) «вековые» воздействия, результирующее влияние которых не меняется;

2) циклические воздействия, влияние которых совершает законченный круг в течение некоторого фиксированного временного промежутка;

3) случайные воздействия, результирующее влияние которых с высокой скоростью меняет направление и интенсивность, индуцируя нерегулярную составляющую в .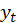

Т.е. закон распределения переменной 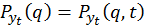зависит от переменной t. Следовательно, от этой переменной зависит и все основные количественные характеристики ряда:

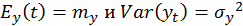
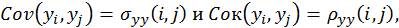
Построим регрессионную модель ряда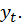

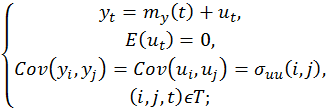
Причём, если 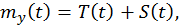т.е. функция регрессии является суммой тренда и сезонной составляющей, то требование стационарности (неизменность функции во времени 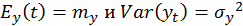) будет нарушено.

Примером временного ряда служит ВВП России. Рассматривая данный пилообразный график, констатируем, что в структуре квартальных уровней ВВП России отчётливо видны: 1)Восходящая тенденция (тренд); 2) Сезонная составляющая; 3) Случайная составляющая;

Принимая в качестве тренда возрастающую линейную функцию времени, приходим к спецификации модели динамики ВВП России:

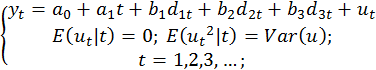
Это линейная модель множественной регрессии (базовая модель эконометрики).

16. Модели тренда временного ряда.

В общем случае в структуре временного ряда можно выделить три составляющих:

1) Тренд (тенденция);

2) Сезонная составляющая;

3) Случайная составляющая.

Отметим простейшие модели тренда:

1) Линейная функция времени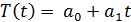

2) Квадратная парабола времени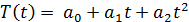

3) Экспоненциальная функция времени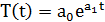

_________

y_t - некоторый временной ряд (датированная экономическая переменная).

Модели временного ряда предназначены для объяснения (прогноза) уровня ряда, y_t фактором времени, t. Это значит, что экзогенной переменной модели временного ряда служит целочисленная переменная t, а эндогенной переменной является уровень ряда, y_t, представленный в виде некоторой функции независимой переменной t. Переменная y_t служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами (движущими силами), оказывающими воздействие на данный объект с ходом времени, которые можно классифицировать следующим образом:

1) «вековые» воздействия, результирующее влияние которых не меняется;

2) циклические воздействия, влияние которых совершает законченный круг в течение некоторого фиксированного временного промежутка;

3) случайные воздействия, результирующее влияние которых с высокой скоростью меняет направление и интенсивность, индуцируя нерегулярную составляющую в .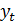

1) Обозначим символом T_t – некоторую монотонную функцию переменной t; в модели временного ряда эта функция будет играть роль тенденции. часто используемые типы тенденции (тренда). Вот пять простейших моделей:

T_t = a₀+a₁∙t, T_t =a₀∙t^a1, T_t =a₀+a₁∙ln(t₀+t), T_t=a₀∙exp(a₁∙t) , T_t=a₀∙exp(-t^a1).