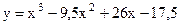Задание: Используя геометрический и физический смыслы производной, решите предложенные задачи
Тема №1 Вычисление пределов функций
Задание: Вычислить пределы функций, не применяя формулу Лопиталя:
1.1 а) 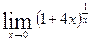 в)
в) 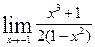
1.2 а) 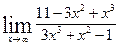 в)
в) 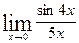
1.3 а) 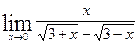 в)
в) 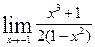
1.4 а) 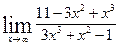 в)
в) 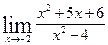
1.5 а) 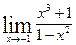 в)
в) 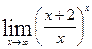
1.6 а) 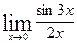 в)
в) 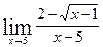
1.7 а) 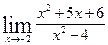 в)
в) 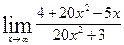
1.8 а) 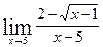 в)
в) 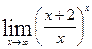
1.9 а) 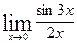 в)
в) 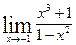
1.10 а) 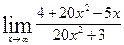 в)
в) 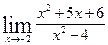
Тема №2 Производная функции
Задание: Продифференцировать функции:
1.1 а) 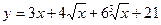 в)
в) 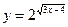
1.2 а) 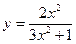 в)
в) 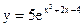
1.3 а) 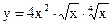 в)
в) 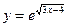
1.4 а) 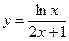 в)
в) 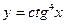
1.5 а) 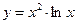 в) y=(5+x2)10
в) y=(5+x2)10
1.6 а) 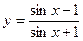 в)
в) 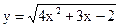
1.7 а) 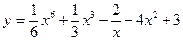 в)
в) 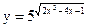
1.8 а) 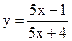 в)
в) 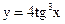
1.9 а) 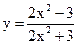 в)
в) 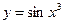
1.10 а) 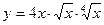 в)
в) 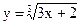
Тема №3. Геометрический и физический смыслы производной функции
Задание: Используя геометрический и физический смыслы производной, решите предложенные задачи.
3.1 Составить уравнение касательной к графику функции у = х2 – 2 в точке с абсциссой, равной 2
3. 2 Какой угол с положительным направлением оси (Ох) составляет касательная, проведённая к графику функции 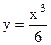 в точке с абсциссой равной (
в точке с абсциссой равной ( 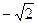 )?
)?
3.3 В какой точке касательная к кривой у = -х2 + 2х - 3 наклонена к оси (Ох) под углом 0о?
3.4 Тело движется прямолинейно по закону S(t) = 0,25t4 – 4t3 + 16t2. Определить моменты остановки этого тела
3.5 Найти скорость и ускорение движения, заданного законом:
S(t) = 0,25t4 – 4t3 + 16t2 для t=2
3.6 Найти скорость и ускорение движения, заданного законом:
S(t) = 5t2 + 4t3 + 16t для момента времени t=2
3.7 Составить уравнение касательной к графику функции у = 2х3 – 3 в точке с абсциссой, равной 1
3.8 Тело движется прямолинейно по закону S(t) = 0,25t4 – 4t3 + 16t. В какой момент времени ускорение этого движения буден равно нулю?
3.9 В какой точке касательная к графику функции у = х2 – х будет наклонена к оси (Ох) под углом 45о?
3.10 В какой точке касательная к графику функции у = х2 –2х будет параллельна оси (Ох)?
Тема №4. Исследование функций средствами дифференциального исчисления. Построение графика.
Задание: Найдите область определения функции, проведите исследование на чётность, монотонность, экстремумы, выпуклость-вогнутость, точки перегиба и постройте график функции:
4.1 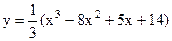
4.2 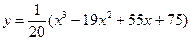
4.3 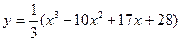
4.4 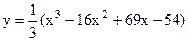
4.5 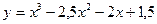
4.6 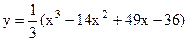
4.7 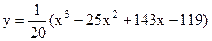
4.8 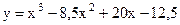
4.9 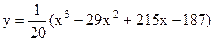
4.10