Проектный расчет рекуперативных теплообменников

До проведения расчета рекуперативных теплообменников производят выбор пространства для движения теплоносителя с целью улучшения условий теплоотдачи со стороны теплоносителя с большим термическим сопротивлением. Для этого жидкость, обладающую большой вязкостью или расход которой меньше, рекомендуется направлять в то пространство, где скорость ее может быть выше. Теплоносители, содержащие загрязнения, направляют в пространства, поверхности которых легче могут быть очищены от отложений. Выбор пространства должен учитывать также потери тепла в окружающую среду.

Предварительно выбирают и направление взаимного движения теплоносителей, учитывая преимущество противотока при теплообмене без изменения агрегатного состояния теплоносителей, а также целесообразность совпадения направлений вынужденного и свободного движения теплоносителя.

Очень важен правильный выбор оптимальных скоростей движения теплоносителей, так как это имеет решающее значение при конструировании и эксплуатации теплообменника. С увеличением скорости потоков 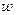увеличивается коэффициент теплопередачи 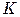, а следовательно, уменьшается необходимая поверхность теплопередачи 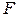, что в свою очередь ведет к уменьшению габаритных размеров теплообменника и его стоимости. Кроме того, с увеличением скорости уменьшается возможность образования отложений на поверхности теплообмена. Однако при чрезмерном повышении скорости движения потока увеличивается гидравлическое сопротивление теплообменника, что приводит к вибрации труб и гидравлическим ударам. Оптимальная скорость определяется из условий достижения желаемой степени турбулентности потока. Обычно стремятся, чтобы скорость потока в трубах соответствовала критерию 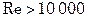. В связи с этим рекомендуются следующие оптимальные скорости движения 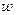(м/с): воды и жидкостей с умеренной вязкостью – 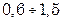; вязких жидкостей – 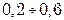; воздуха и газов при умеренном давлении – 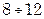; насыщенного пара под давлением – 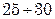; насыщенного пара под вакуумом – 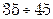. Наиболее желателен выбор оптимальной скорости на основе технико-экономического расчета.

Полный расчет теплообменника включает тепловой, конструктивный и гидравлический расчеты.

Тепловой расчет. Тепловой расчет проектируемых теплообменников производят в следующей последовательности:

– рассчитывают тепловую нагрузку и расход теплоносителей;

– рассчитывают средний температурный напор и средние температуры теплоносителей;

– рассчитывают коэффициент теплопередачи и поверхность теплообмена.

Наиболее прост расчет при постоянных температурах теплоносителей по длине теплообменника. В этом случае физические свойства теплоносителей и разность температур постоянны и расчет сводится к определению коэффициента теплопередачи. Близкие к этим условиям наблюдаются в обогреваемых конденсирующимся паром кипятильниках. В общем случае температуры теплоносителей изменяются по длине теплообменника. Взаимосвязь изменений температур теплоносителей определяется условиями теплового баланса, который для бесконечно малого элемента теплообменника имеет вид:

,

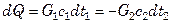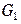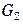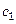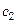где , и , – расходы и теплоемкости теплоносителей, а 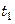и 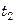– их температуры в произвольном сечении аппарата.

Уравнение теплового баланса для всего аппарата без учета потерь тепла получают путем интегрирования последнего уравнения:

,

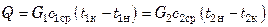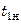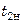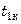где и , и 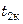– начальные и конечные температуры теплоносителей; 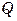– тепловая нагрузка.

Расходы теплоносителей при теплообмене без изменения агрегатного состояния на основании теплового баланса:

;

.

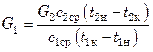При изменении агрегатного состояния теплоносителя уравнение теплового баланса может иметь различную форму в соответствии с условиями протекания процесса. Например, при конденсации пара

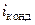( – расход пара; и – энтальпии пара и конденсата).

Изменение энтальпии

,

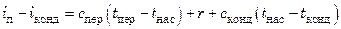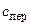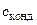где и – средние удельные теплоемкости перегретого пара и конденсата; 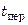и 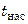– температуры перегретого и насыщенного пара.

Если неизвестна конечная температура одного из теплоносителей, то ее определяют из теплового баланса. Когда же неизвестны конечные температуры обоих теплоносителей, то для их определения используют общий прием – метод последовательных приближений. Этот метод основан на том, что вначале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется правильность этого выбора, принимаются уточненные значения указанных параметров и расчет повторяется до получения результатов с желаемой степенью точности. При этом следует принять во внимание, что разность температур между теплоносителями на конце теплообменника должна быть не менее 10–20 °С для жидкостных подогревателей и 5–7 °С для паро-жидкостных подогревателей.

Определение среднего температурного напора 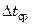производится с учетом характера изменения температур вдоль поверхности теплообмена 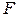. При противотоке, а также при постоянной температуре одного из теплоносителей среднюю разность температур определяют как среднелогарифмическую из большей и меньшей разности температур теплоносителей на концах теплообменника:

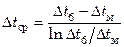
или при .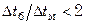

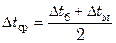При всех других схемах течения среднюю разность температур находят по этим же уравнениям, но с введением поправочного коэффициента (см. раздел 7.7.3).

Среднюю температуру теплоносителя с меньшим перепадом температур по длине аппарата рекомендуется рассчитывать как среднеарифметическую, а среднюю температуру другого теплоносителя находят по известной величине 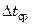, пользуясь соотношением

,

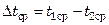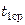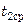где и – средние температуры теплоносителей.

Дальнейшей задачей расчета является нахождение коэффициента теплопередачи 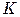. Если теплопередача происходит через плоскую стенку или тонкую цилиндрическую, то

.

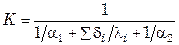Для расчета 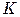необходимо предварительно вычислить коэффициенты теплоотдач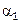и и 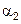по обе стороны теплопередающей стенки, а также термическое сопротивление стенки 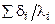, которое включает помимо термического сопротивления самой стенки еще и термические сопротивления загрязнений с обеих ее сторон. Термические сопротивления стенки и слоев загрязнений находят в зависимости от их толщины и коэффициентов теплопроводности материала стенки и загрязнений. Коэффициенты теплоотдачи рассчитывают в зависимости от условий теплоотдачи по одному из уравнений, приведенных в разделе 7.6.

Учитывая многообразие гофрированных поверхностей в пластинчатых теплообменниках, Л.Л. Товажнянским и П.А. Капустенко предложена зависимость для расчета коэффициента теплоотдачи, учитывающая угол наклона гофр по отношению к направлению потока рабочей среды:

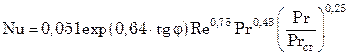, (8.20)

где j – угол наклона гофр.

Это уравнение справедливо в пределах .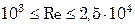

Для расчета теплоотдачи в каналах, образуемых пластинами типа 0,3р, 0,6р и 1,0(см. табл. 8.1), уравнение (8.20) может быть представлено в виде:

при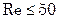

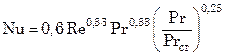; (8.21)

при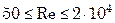

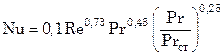. (8.22)

Теми же авторами предложена формула для расчета теплоотдачи в щелевидных каналах по данным о гидравлическом сопротивлении в диапазоне чисел Рейнольдса Re = 10³–2,5·10⁴ и Прандля Pr = 0,5–20:

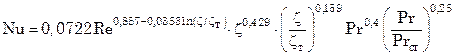, (8.23)

где 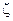–коэффициент гидравлического сопротивления щелевидного канала; 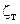– коэффициент гидравлического сопротивления гладкой трубы.

При конденсации быстродвижущегося пара (Re > 300) в каналах сетчато-поточного типа Л.Л. Товажнянский и П.А. Капустенко, используя модель движения дисперсно-кольцевого типа, получили следующую зависимость:

,

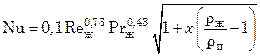где Nu – критерий Нуссельта для пленки конденсата; Re_ж – критерий Рейнольдса, рассчитанный по полному расходу парожидкостной смеси и вязкости жидкой фазы; 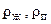– плотности жидкости и пара соответственно; 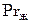– критерий Прандтля для жидкой фазы.

Поскольку коэффициенты теплоотдачи являются функциями скоростей движения, то, чтобы найти их, необходимо знать площади поперечного сечения каналов, по которым движутся теплоносители (расходы известны). Это требует предварительно задаться конструкцией и размерами теплообменника. Помимо этого, для вычисления коэффициента теплоотдачи 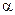часто необходимо знать температуру стенки 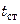или удельную тепловую нагрузку 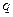, значения которых, в свою очередь, зависят от определяемой величины 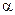. В таких случаях коэффициенты теплоотдачи рассчитывают методом последовательных приближений: величинам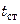и и 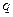задаются и после определения величины коэффициента теплопередачи 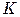проверяют. Для упрощения расчета можно воспользоваться графоаналитическим методом, при котором ведут два параллельных расчета для двух выбранных значений 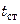со стороны одного из теплоносителей.

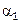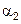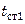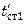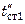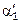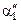Так, например, если коэффициенты теплоотдачи и зависят от температуры стенки , то, задавшись двумя значениями и , вычисляют соответствующие значения и и удельные тепловые нагрузк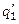и и :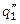

;

,

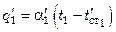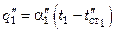где 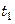– средняя температура теплоносителя.

По величине термического сопротивления стенки 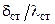рассчитывают температуру стенки со стороны другого теплоносителя:

,

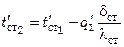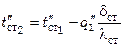
и определяют 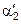и 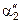, а также 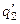и :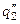

,

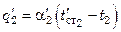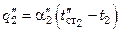
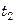( – средняя температура второго теплоносителя).

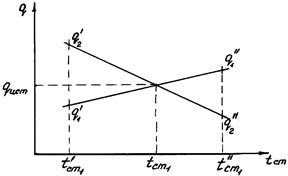Рисунок 8.34 – Зависимость q1 и q2 от значений tст1

Затем строят график зависимост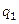и и 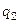от принятых значений 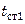(рис. 8.34). По точке пересечения линий, соединяющих тепловые нагрузки при различных значениях 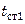, определяют истинные температуру стенки 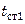и тепловую нагрузку .

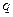Тогда коэффициент теплопередачи .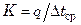

Величина поверхности теплообмена из общего уравнения теплопередачи

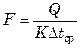, либо .

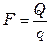Особенности теплового расчета холодильников и конденсаторов. Расчет холодильников-конденсаторов имеет свои особенности, обусловленные характером изменения температур и коэффициентов теплопередачи вдоль поверхности теплопередачи.

На рис. 8.35 показано примерное распределение температур в конденсаторе-холодильнике, в который поступают пары в перегретом состоянии.

В данном случае можно выделить три зоны: I – охлаждение паров до температуры насыщения; II – конденсация паров и III – охлаждение конденсата. В первой зоне пары охлаждаются от температуры до и переходят в насыщенное состояние. Коэффициент теплопередачи для этой зоны имеет меньшую величину, чем в зоне II, где происходит конденсация паров. В зоне III коэффициент теплопередачи имеет промежуточное значение.

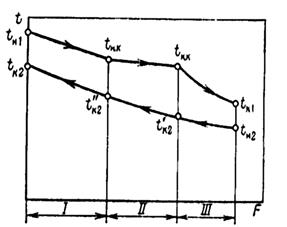Рисунок 8.35 – Профиль температур в конденсаторе-холодильнике

Тепловой баланс по зонам при условии полной конденсации насыщенного пара в количестве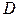

,

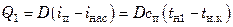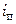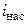где и – энтальпия перегретого и насыщенного пара соответственно; 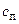–удельная теплоемкость пара;

,

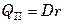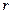– удельная теплота парообразования;

,

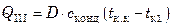здесь 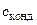и 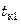– удельная теплоемкость и температура конденсата.

Общая тепловая нагрузка на конденсатор

.

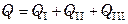Температуры охлаждающего агента (воды) 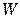в начале и конце зоны II определяют из уравнений теплового баланса

;

,

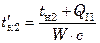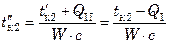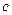( – удельная теплоемкость охлаждающего агента).

Общий расход охлаждающего агента

.

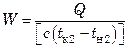Для каждой зоны по известным уравнениям рассчитывают среднюю разность температур 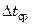и коэффициент теплопередачи .

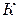Тогда поверхности теплообмена зон:

; ; .

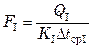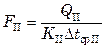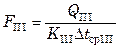Конструктивный расчет. Задачей конструктивного расчета теплообменных аппаратов является определение основных размеров аппаратов и выбор их общей компоновки. Исходными данными для конструктивного расчета являются результаты теплового расчета: расходы теплоносителей, скорости их движения, начальные и конечные температуры, поверхность теплообмена.

Для трубчатых аппаратов конструктивный расчет сводится к определению числа или длины труб, размещению их в трубной решетке (с учетом числа ходов) и нахождению диаметра и высоты аппарата. Расчету подлежат также диаметры патрубков штуцеров теплообменника.

Общее число труб теплообменника 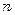при их среднем диаметре 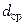и принятой длине 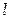определяют по поверхности теплообмена

.

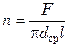При заданном расходе жидкости 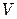и принятой скорости ее движения 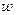по трубам с внутренним диаметром 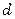число труб одного хода

.

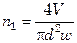Число ходов в трубном пространстве теплообменника

.

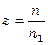В многоходовых аппаратах рекомендуется выбирать четное число ходов, тогда отвод и подвод теплоносителя к теплообменнику осуществляется у одной крышки.

Внутренний диаметр кожуха теплообменника 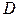определяется числом трубок, размещаемых в трубной решетке. Отверстия для труб в трубных решетках размещают равномерно по всему сечению. Такое размещение сравнительно легко осуществляется в одноходовом теплообменнике. В многоходовых теплообменниках, имеющих перегородки, размещение труб производят обычно графическим путем. По геометрической конфигурации различают размещение трубок по вершинам правильных многоугольников и по концентрическим окружностям.

При размещении труб шаг 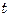принимают в зависимости от их наружного диаметра 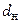, при закреплении труб развальцовкой 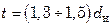, а при закреплении их сваркой 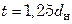. Общее число труб 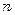, которое можно разместить на трубной доске по вершинам равносторонних треугольников в пределах вписанного в круг шестиугольника,

,

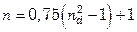где 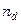– число труб, размещающихся на диаметре трубной решетки:

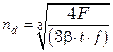
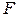( – расчетная поверхность теплопередачи; 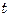– шаг труб; 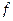– поверхность 1 м трубы принятого диаметра; b – отношение высоты 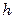или длины 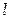рабочей части теплообменника к его диаметру ).

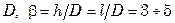Диаметр трубной решетки или внутренний диаметр кожуха теплообменника

.

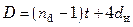Рабочая длина 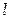одной трубы

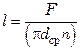, или .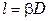

Полная высота теплообменника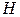

,

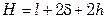где 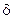– толщина трубной решетки (для стальных труб 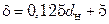мм, для медных труб 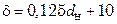мм); 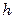– высота камеры (крышки), 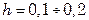м.

Змеевики располагают в аппаратах таким образом, чтобы они по всей высоте находились в жидкости и со всех сторон не доходили до стенок аппарата на 0,25 – 0,4 м.

При известном внутреннем диаметре аппарата 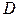диаметр витка змеевика 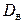составит

.

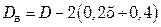Общая длина труб змеевика

.

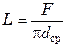Длина одного витка 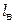змеевика

.

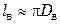Число витков 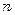змеевика определяют из зависимости

,

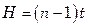где 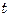– расстояние между витками по вертикали, .

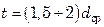Для пластинчатых теплообменников при конструктивном расчете определяют: размеры пластин и число каналов в одном пакете, число пластин в каждом пакете и число пакетов в аппарате, общее число пластин и основные размеры аппарата.

Число параллельных каналов в пакете для каждой среды

,

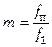где 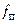– площадь поперечного сечения пакета, 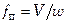( 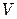– объемный расход теплоносителя, 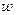– его скорость); 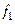– площадь сечения одного межпластинчатого канала.

Полученное значение 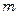округляют до целого.

Число пластин в пакете

.

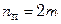В крайних пакетах, соприкасающихся с плитами, общее число пластин на одну больше (концевую):

.

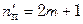Поверхность теплопередачи одного пакета

,

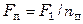где 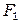– поверхность теплопередачи одной пластины.

Число пакетов (ходов) в теплообменнике

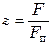
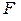( – рабочая поверхность аппарата, найденная при тепловом расчете).

Если величина 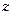получается дробной, то ее округляют до целого числа и корректируют соответственно поверхность всего аппарата:

.

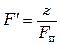Общее число пластин в аппарате (секции)

.

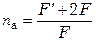Гидравлический расчет теплообменников. Целью гидравлического расчета является определение сопротивления, создаваемого теплообменником, и мощности, необходимой для перемещения через него жидкости.

Гидравлическое сопротивление теплообменника 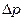складывается из потерей давления на преодоление трения 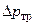и потери давления 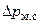, расходуемого на преодоление местных сопротивлений

.

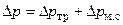Для кожухотрубчатых теплообменников полное гидравлическое сопротивление трубного пространства

,

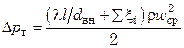где 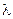– коэффициент внешнего трения (см. раздел 1.3.4); 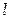– общая длина пути потока в трубах; 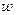– скорость потока в трубах; 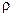– плотность потока при его средней температуре; 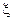– коэффициент местного сопротивления.

Гидравлическое сопротивление межтрубного пространства

.

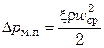Здесь 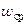– средняя скорость движения теплоносителя в межтрубном пространстве; 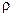– его плотность при средней температуре; 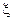– коэффициент сопротивления для межтрубного пространства (для теплообменников с длиной труб 6 м величина 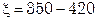; при длине труб 3 и 9 м принимают поправочные коэффициенты 0,5 и 1,5 соответственно).

Гидравлическое сопротивление многопакетного пластинчатого теплообменного аппарата при одинаковом числе каналов во всех пакетах

,

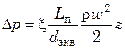либо

,

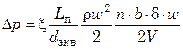где 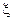– коэффициент общего гидравлического сопротивления единицы относительной длины межпластинчатого канала; 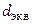и 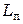– эквивалентный диаметр и приведенная длина одного межпластинного канала, 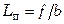( 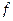– рабочая поверхность теплообмена одной пластины; 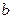– ширина рабочей части пластины); 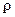– плотность теплоносителя при его средней температуре; 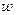– его скорость в межпластинном канале; 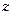– число последовательно включенных каналов или число пакетов в секции для данной рабочей среды; 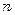– общее число пластин в секции (аппарате); 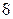– зазор между пластинами; 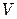– объемная производительность аппарата.

При турбулентном течении (10³ < Re < 2,5·10⁴) в каналах, образованных гофрированными пластинами, коэффициент гидравлического сопротивления

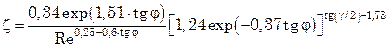, (8.25)

где 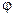– угол наклона гофра; 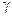– угол при вершине гофра.

Для пластин типа 0,3р, 0,6р и 1,0(см. табл. 8.1):

при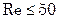

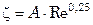; (8.26)

при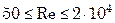

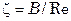. (8.27)

Значения коэффициентов A и B в уравнениях (8.26) и (8.27) приведены в таблице 8.2.

Таблица 8.2 – Значения коэффициентов A и B в уравнениях (8.26) и (8.27)

Величина	Типы пластин
0,3р	0,6р	1,0
A	19,3	12,0	7,0
B			—

Между теплопередачей и потерей давления существует тесная физическая и экономическая связь, обусловленная скоростью движения теплоносителей. Чем больше скорости теплоносителей, тем выше коэффициент теплопередачи и тем компактнее для данной тепловой нагрузки теплообменный аппарат, а следовательно, меньше капитальные затраты. Но при этом растет гидравлическое сопротивление потоку и возрастают эксплуатационные расходы. Поэтому скорость теплоносителя выбирается в некоторых оптимальных пределах, определяемых, с одной стороны, стоимостью поверхности теплообмена аппарата данной конструкции, а с другой – стоимостью затрачиваемой энергии при эксплуатации аппарата.