Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к убыли энергии системы, что приводит к затуханию колебаний. Чаще всего сила сопротивления F_C пропорциональна величине скорости:

,

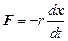где r – постоянная, называемая коэффициентом сопротивления. Знак минус указывает на то, что сила сопротивления направлена противоположно направлению скорости.

Уравнение второго закона Ньютона для одномерного пружинного маятника при наличии сил сопротивления имеет вид:

.

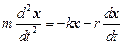Примем обозначения:

.

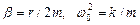Уравнение (21.7) в проекции принимает вид:

.

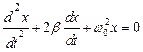Это дифференциальное уравнение описывает затухающие колебания. Параметр b характеризует скорость затухания колебаний и называется коэффициентом затухания, w₀ – собственная частота колебаний системы.

Решением уравнения (21.9) при малом затухании (b<w₀) является уравнение вида:

,

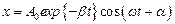где A₀ – максимальная амплитуда колебаний, a – начальная фаза,

частота колебаний .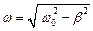

Движение системы, описываемое уравнением (21.10), строго говоря, не является периодическим. Но его можно условно рассматривать как гармонические колебания частоты w с амплитудой, изменяющейся по закону

.

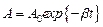По аналогии со свободными колебаниями можно ввести период затухающих колебаний Т

.

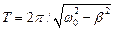Скорость затухания колебаний характеризуется, отношением амплитуд, соответствующих моментам времени, отличающимся на период. Эта величина называется декрементом затухания

_.

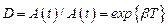Часто для характеристики колебаний системы используют логарифмический декремент затухания, определяемый следующим образом:

_.

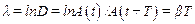Используя логарифмический декремент затухания закон убывания амплитуды со временем можно записать в виде:

.

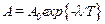Из (21.14) следует формула для нахождения логарифмического декремента затухания:

,

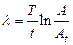где Т – период колебаний, t- промежуток времени, за который амплитуда колебаний изменилась от A до A_t.