Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Начнем.
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами 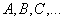
Пример: рассмотрим матрицу «два на три»:
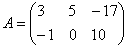
Данная матрица состоит из шести элементов:
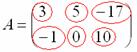
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
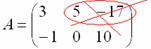
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
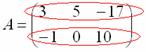
и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют
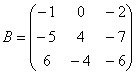
квадратной, например: – матрица «три на три».
Если в матрице один столбец 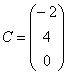 или одна строка
или одна строка 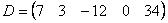 , то такие матрицы также называют векторами.
, то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: 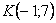 . По существу, координаты точки
. По существу, координаты точки 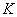 записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение:
записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: 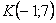 и
и 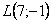 – это две совершенно разные точки плоскости.
– это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
