Энтропийное значение погрешности

При пратическом использовании изложенного информационного подхода для оценки точности результатов измерения привычнее оперировать не со значением энтропийного интервала неопределённости результата измерения d, а с половиной этого интервала, присвоив ей, наименование энтропийного значения погрешности .
Формальным определением энтропийного значения погрешности являются соотношения

(22)

Отсюда

(23)

(24)

Найдём энтропийное значение погрешности с нормальным распределением

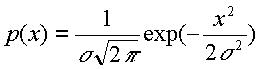
В (19) получено

Тогда

(25)

Найдём энтропийное значение погрешности с равномерным распределением в интервале ± .
В (13) найдено, что

Тогда

(26)

Найдём энтропийное значение погрешности с распределением Симпсона. В (21) найдено

Тогда

(27)

Из выражений (25),(26),(27) видно, что энтропийное значение погрешности зависит от СКО погрешности и от её распределения. Величиной, характеризующей дезинформационное действие погрешности, является энтропийный коэфициент , равный

(28)

Тогда для нормального распределения н=2,07, для равномерного распределения р=1,73, для распределения Симпсона т=2,02. Установлено, что наибольшее дезинформационное действие оказывает погрешность с нормальным распределением.

ΙΙ

2.1 Математичиская модель ЦСИ или уравнение измерения …………………………………1

2.2 Представление дискретизованного сигнала во временной области……………………..4

2.3 Спектр дискретизованного сигнала…………………………………………………………….7

2.4 Спектр дискретизированного сигнала при различных между верхней частотой в спектре сигнала и частотой дискретизации……………………………………………………….8

2.5 Виды восстановления непрерывного сигнала из дискретизированного…………………11

2.6 Восстановление дискретизированного сигнала с помощью ряда Котельникова……….12

2.7 Восстановление дискретизированного сигнала с помощью степенных полиномов, погрешности аппроксимации, определение частоты дискретизации. Виды аппроксимации, погрешность аппроксимации…………………………………………………………………………16

2.8. Ступенчатая аппроксимация……………………………………………………………………17

2.9 Кусочно-линейная аппроксимация……………………………………………………………...19

2.10 Общий подход к оцениванию суммарной погрешности СИ………………………………..21

2.11 Уравнение погрешности без использования линеаризации………………………………..23

2.12 Уравнение погрешности с использованием линеаризации……………………………....24

2.13-2.14 Оценивание систематической и случайной составляющей погрешности СИ…...27

2.15 Вычисление суммарной погрешности средства измерений с линеаризацией равнений погрешности …………………………………………………………………………………………….29

2.16 Вычисление суммарной погрешности средства измерений без линеаризацией равнений погрешности………………………………………………………………………………...30

2.17 Метрологические исследования вычислительного компонента,………………………...32

2.18 Характеристики вычислительного компонента, определяемые при аттестации ……..34

2.19 Анализ составляющих погрешности вычислительного компонента…………………….36

2.20 Оценивание трансформированной погрешности алгоритма …………………………….39

2.21 Оценивание погрешности округления в вычислениях …………………………………….47

2.22 Оценивание погрешности вычисления ВК с алгоритмом косвенного измерения…….50

2.23 Понятие и свойства энтропии ………………………………………………………………….54

2.24 Энтропийный интервал неопределённости…………………………………………………..56

2.25 Энтропийное значение погрешности…………………………………………………………...57