Бесконечно большие функции и их свойства
Определение. Функция y=F(x) называется бесконечно большой (б.б.) при x® a, если
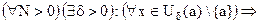
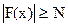 .
.
Это обозначается символом 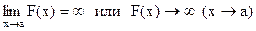 , хотя предел этой функций при
, хотя предел этой функций при 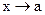 не существует.
не существует.
Пример. Функция 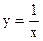 является б.б. функцией при
является б.б. функцией при 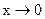 , так как
, так как
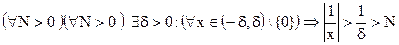 .
.
Очевидно, что любая б.б. функция не ограничена в окрестности точки 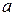 .
.
Если 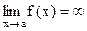 и в некоторой окрестности точки а функция
и в некоторой окрестности точки а функция 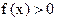 (соответственно
(соответственно 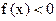 ), то еще пишут
), то еще пишут 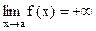 (соответственно
(соответственно 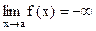 ).
).
Отметим следующие свойства б.б. функций.
1) Сумма двух б.б. одного знака при 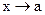 является б.б. при
является б.б. при 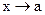 .
.
2) Сумма б.б. функции при 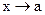 и ограниченной в окрестности точки а функции является б.б. при
и ограниченной в окрестности точки а функции является б.б. при 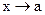 .
.
Пример. 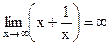 ,так как х- есть б. б. при
,так как х- есть б. б. при 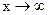 , а
, а 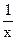 б. м., следовательно, ограниченная функция при
б. м., следовательно, ограниченная функция при 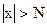 .
.
3) Если 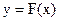 б. б. при
б. б. при 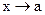 , а
, а 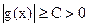 в некоторой окрестности точкиа, то функция
в некоторой окрестности точкиа, то функция 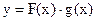 является б. б. при
является б. б. при 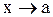 . В частности, произведение двух б. б. и произведение б. б. на функцию, имеющую ненулевой предел, является б. б.
. В частности, произведение двух б. б. и произведение б. б. на функцию, имеющую ненулевой предел, является б. б.
Пример. 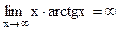 , так как х – б.б. и
, так как х – б.б. и 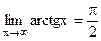 .
.
4) Если 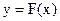 б. б. при
б. б. при 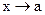 , то
, то 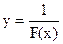 б.м. при
б.м. при 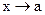 .
.
5) Если 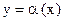 б.м. при
б.м. при 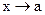 и
и 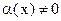 при
при 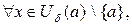 то
то 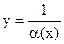 является б.б. при
является б.б. при 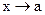 .
.
Пример: 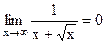 , так как
, так как 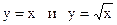 б. б. одного знака при
б. б. одного знака при 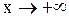 .
.
3.3 Сравнение бесконечно малых и бесконечно больших
Определение. Бесконечно малая 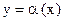 называется б.м. высшего порядка малости по сравнению с б.м.
называется б.м. высшего порядка малости по сравнению с б.м. 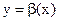 при
при 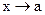 в случае, если найдётся б.м.
в случае, если найдётся б.м. 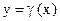 при
при 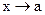 такая, что
такая, что 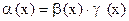 . Соответствующее обозначение
. Соответствующее обозначение 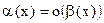 .
.
Пример: При 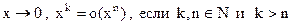 , так как
, так как 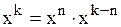 и
и 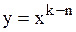 есть б.м. при
есть б.м. при 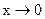 .
.
При 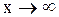 :
: 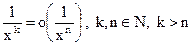
Определение. Бесконечно малые 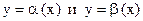 при
при 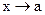 называются эквивалентными, если
называются эквивалентными, если 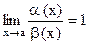 . Обозначение
. Обозначение 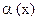 ~
~ 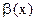 . Подобное определение даётся и для б.б. функции.
. Подобное определение даётся и для б.б. функции.
Пример. Б.м. 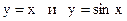 эквивалентны при
эквивалентны при 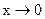 , это следует из первого замечательного предела.
, это следует из первого замечательного предела.
Это отношение эквивалентности удовлетворяет трём свойствам
1) 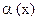 ~
~ 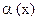 ;
;
2) 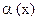 ~
~ 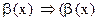 ~
~ 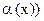 ;
;
3) Если 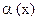 ~
~ 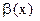 и
и 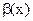 ~
~ 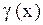 , то
, то 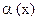 ~
~ 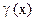 .
.
Теорема. Из 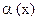 ~
~ 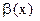 следует, что
следует, что 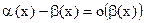 .
.
Теорема. Пусть 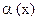 есть б. м. при
есть б. м. при 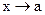 , тогда:
, тогда:
1) 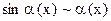 ;
;
2) 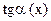 ~
~ 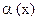 ;
;
3) 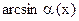 ~
~ 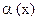 ;
;
4) 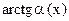 ~
~ 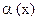 ;
;
5) 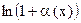 ~
~ 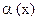 ;
;
6) 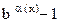 ~
~ 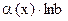 ,
, 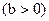 ;
;
7) 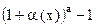 ~
~ 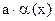 .
.
Эти эквивалентные б.м. позволяют более просто вычислять некоторые пределы с помощью следующей теоремы.
Теорема. Пусть 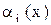 ~
~ 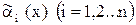 при
при 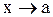 , тогда
, тогда
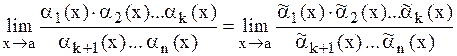 .
.
При этом оба записанных предела существуют одновременно. Если одно из выражений б. б., то другое также является б. б.
Пример. 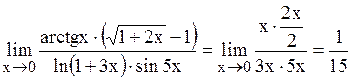 ,
,
так как 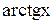 ~
~ 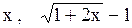 ~
~ 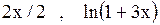 ~
~ 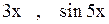 ~
~ 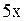 .
.
Непрерывность функции
Определение. Функция 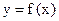 называется непрерывной в точке
называется непрерывной в точке 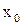 , если выполняются три условия:
, если выполняются три условия:
1) существует 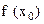 ;
;
2) существует 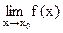 ;
;
3) 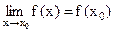 .
.
В символической форме это определение записывается так:
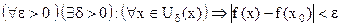 .
.
Функция 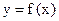 называется непрерывной в точке
называется непрерывной в точке 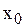 слева (справа), если выполняются три условия:
слева (справа), если выполняются три условия:
1) 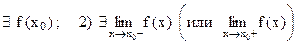 ;
;
2) 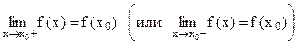 .
.
Очевидно, что функция является непрерывной в точке 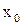 в том и только в том случае, когда она непрерывна в этой точке слева и справа.
в том и только в том случае, когда она непрерывна в этой точке слева и справа.
График непрерывной функции представляет из себя непрерывную линию.
Теорема (о непрерывности монотонной функции). Пусть функция 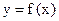 монотонна (монотонно возрастает или монотонно убывает) на отрезке [а,
монотонна (монотонно возрастает или монотонно убывает) на отрезке [а, 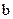 ] и принимает все значения из отрезка
] и принимает все значения из отрезка 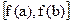 , тогда она непрерывна в каждой точке интервала (а,
, тогда она непрерывна в каждой точке интервала (а, 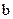 ), непрерывна в точке а справа и в точке
), непрерывна в точке а справа и в точке 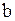 слева. (рис.9)
слева. (рис.9)
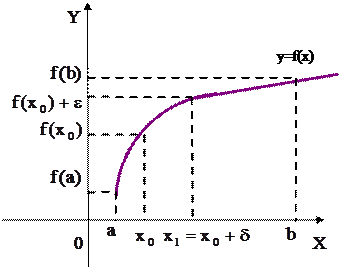 |
Рис. 9
Из этой теоремы следует, что все основные элементарные функции непрерывны во всех внутренних точках своей области определения, а во всех граничных точках области определения, принадлежащих ей, они непрерывны справа и слева. Это следует из того, что любую точку из области определения основной элементарной функции можно включить в отрезок, где эта функция монотонна и принимает все значения из отрезка 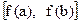 .
.
Например, функция 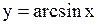 непрерывна во всех точках интервала
непрерывна во всех точках интервала
(–1,1), непрерывна в точке 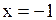 справа и в точке
справа и в точке 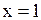 слева, так как оно монотонно возрастает в
слева, так как оно монотонно возрастает в 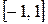 и для
и для
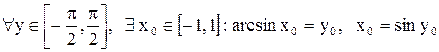 .
.
ТеоремаПусть функции 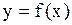 и
и 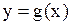 непрерывны в точке
непрерывны в точке 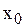 . Тогда функции
. Тогда функции
1) 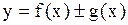 , 2)
, 2) 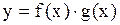 , 3) при
, 3) при 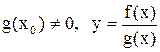 .
.
также непрерывны в точке 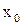 .
.
Теорема (непрерывность сложной функции). Пусть функция 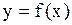 непрерывна в точке
непрерывна в точке 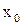 и
и 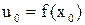
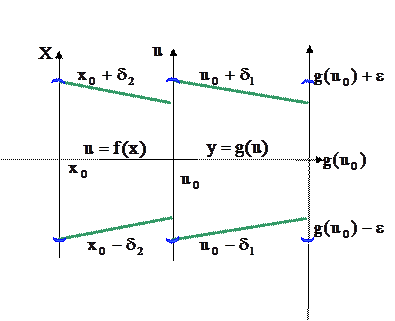 , а функция
, а функция 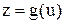 непрерывна в точке
непрерывна в точке 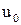 . Тогда сложная функция
. Тогда сложная функция 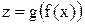 непрерывна в точке
непрерывна в точке 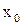 .
.
Рис. 10
Следствие 1. Если 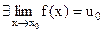 и функция
и функция 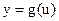 непрерывна в точке
непрерывна в точке 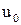 , то
, то 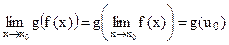 .
.
Пример. 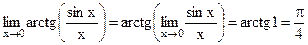 .
.
Следствие 2. Любая элементарная функция непрерывна во всех внутренних точках своей области определения, а в граничных точках отрезков области определения непрерывна справа или слева.
Это следует из теорем 1, 2, 3.
