Диффузионная теория выпрямления запорного слоя Шоттки
В диффузионной теории выпрямления запорного слоя Шоттки предполагается, что 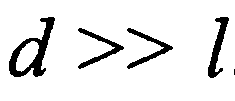 Это неравенство выполняется при малой подвижности и низкой концентрации электронов и означает, что носитель заряда, проходя ОПЗ, испытывает многократные столкновения с тепловыми колебаниями атомов полупроводника. Поскольку в ОПЗ существует и градиент концентрации электронов и электрическое поле, то при записи выражения для плотности тока в этом случае необходимо учитывать как диффузионную, так и дрейфовую составляющие тока, т.е.
Это неравенство выполняется при малой подвижности и низкой концентрации электронов и означает, что носитель заряда, проходя ОПЗ, испытывает многократные столкновения с тепловыми колебаниями атомов полупроводника. Поскольку в ОПЗ существует и градиент концентрации электронов и электрическое поле, то при записи выражения для плотности тока в этом случае необходимо учитывать как диффузионную, так и дрейфовую составляющие тока, т.е.
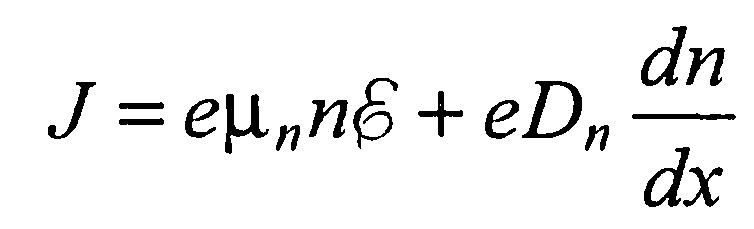 (35)
(35)
где Dn - коэффициент диффузии электронов. При записи плотности тока в таком виде предполагается, что напряженность электрического поля в запорном слое мала, вследствие чего дрейфовая скорость движения электронов 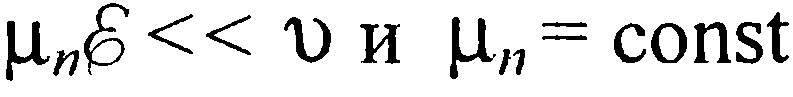
Для нахождения вольтамперной характеристики уравнение (35) решается при следующих граничных условиях:
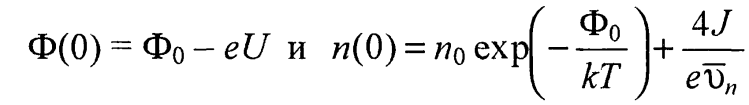 (36)
(36)
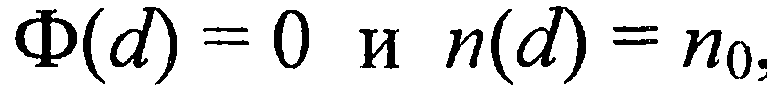 (37)
(37)
где 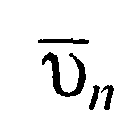 средняя тепловая скорость электронов. Второе соотношение в граничных условиях (36) требует специального обоснования. Запишем плотность тока через разность плотностей потоков электронов
средняя тепловая скорость электронов. Второе соотношение в граничных условиях (36) требует специального обоснования. Запишем плотность тока через разность плотностей потоков электронов 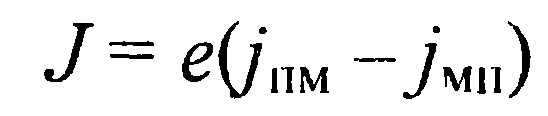 Из выражения (27) с учетом того, что средняя тепловая скорость электронов
Из выражения (27) с учетом того, что средняя тепловая скорость электронов 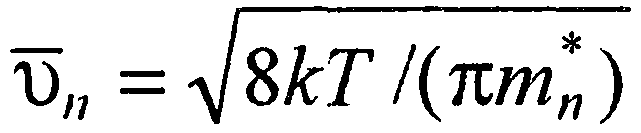 , а
, а 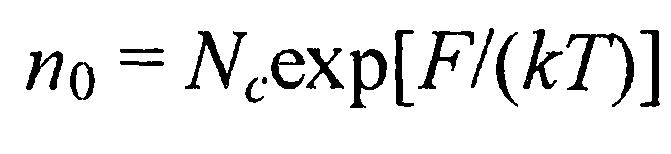 будем иметь
будем иметь
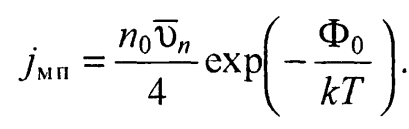 (38)
(38)
Аналогичное выражение можно записать и для jнм , заменив концентрацию электронов на поверхности полупроводника в равновесных условиях 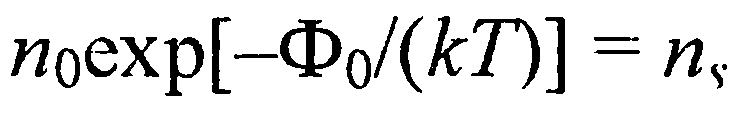 на концентрацию
на концентрацию 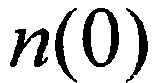 при наличии тока через контакт. Тогда
при наличии тока через контакт. Тогда
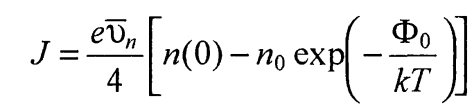 (39)
(39)
Отсюда получается выражение для n0 в граничных условиях (36).
Домножая обе части равенства (35) на ехр[Ф(х)/(кТ)] и принимая во внимание, что 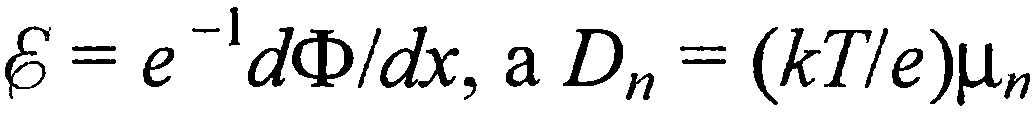 , получим
, получим
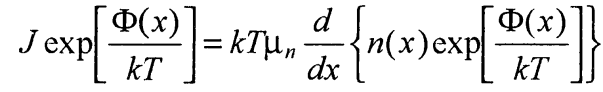 (40)
(40)
Теперь проинтегрируем соотношение (40) в пределах от 0 до d, учитывая будем иметь
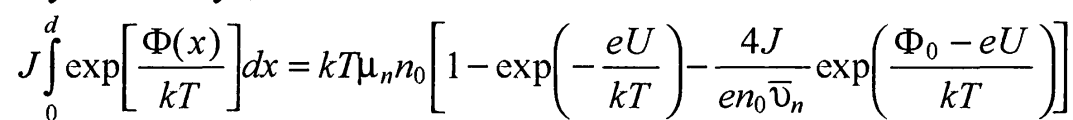 (41)
(41)
Отсюда
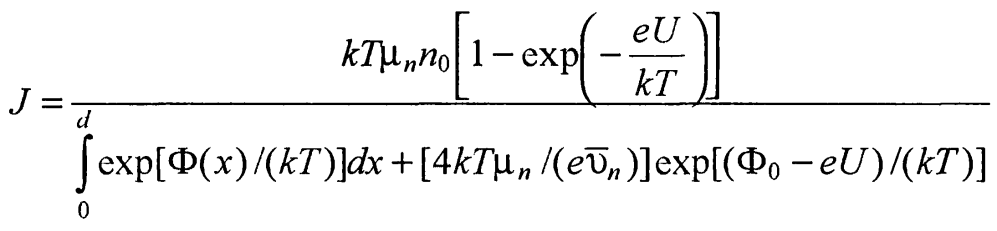 (42)
(42)
Для слоя Шоттки Ф(х) задается формулой (19) и точное значение интеграла в знаменателе выражения (42) может быть получено только численным способом. Чтобы получить аналитическое выражение для вольтамперной характеристики, проведем приближенное вычисление этого интеграла. Поскольку Ф(х) быстро убывает с увеличением х.
соотношение (19), то значение рассматриваемого интеграла в основном определяется областью вблизи плоскости х = 0. С учетом этого разложим Ф(х) в ряд по х, ограничиваясь линейным приближением
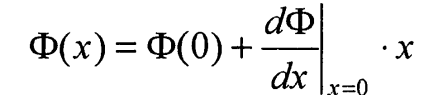 (43)
(43)
В соответствии с соотношением (20)
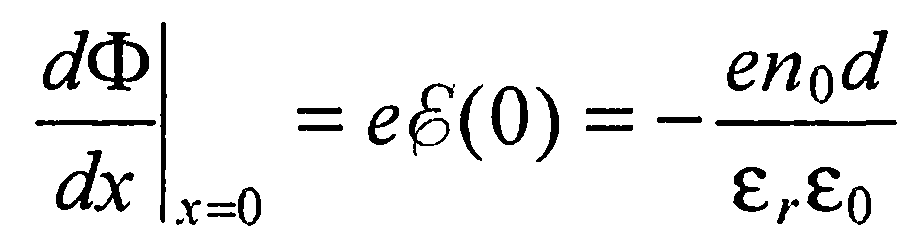 (44)
(44)
После подстановки выражений для 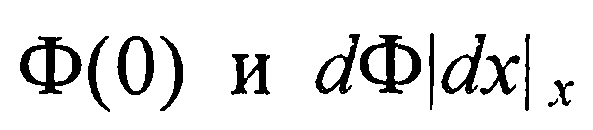 в соотношение (43) получим
в соотношение (43) получим
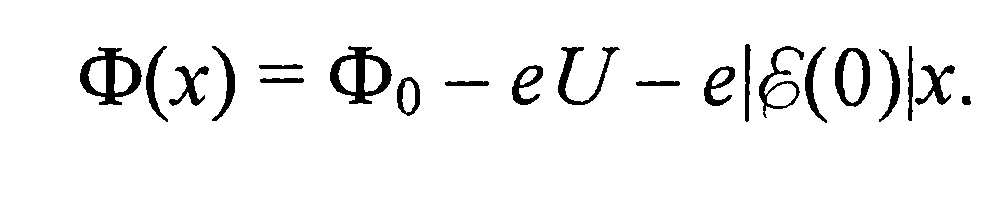 (45)
(45)
Тогда
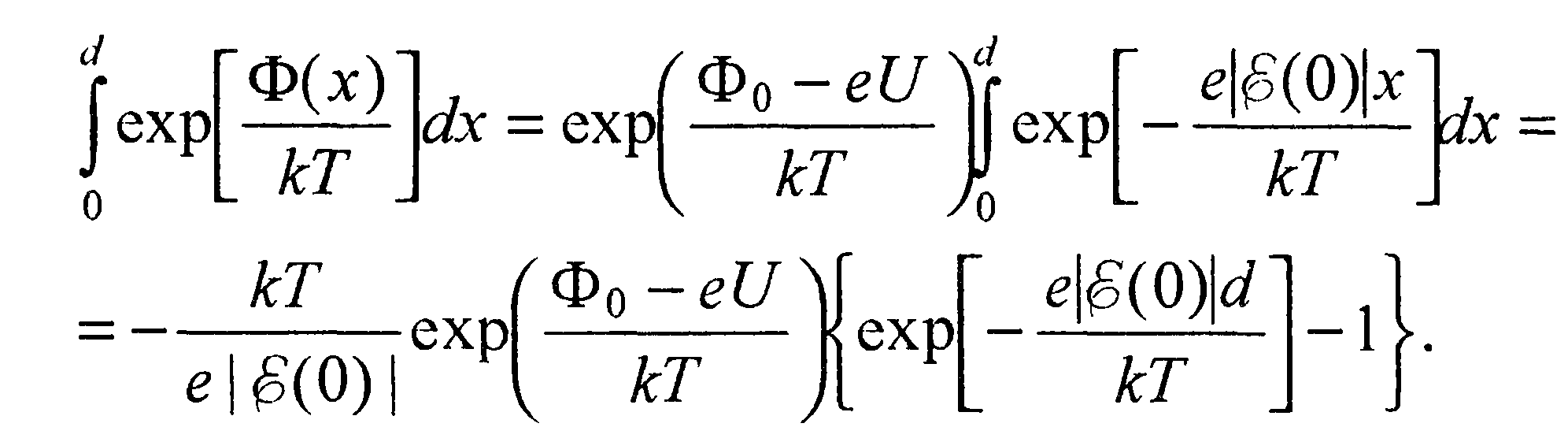 (46)
(46)
Из соотношений (24) и (44) следует, что
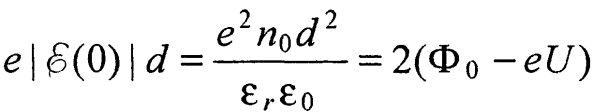 (47)
(47)
Если учесть, что запорный слой существует пока изгиб зон достаточно велик и 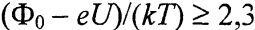 ,то
,то
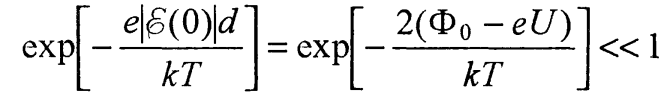 (48)
(48)
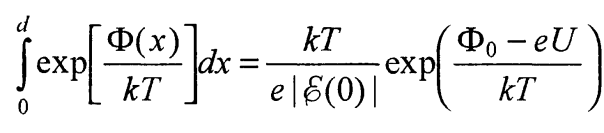 (49)
(49)
Подстановка равенства (49) в (42) после несложных преобразований приводит к выражению
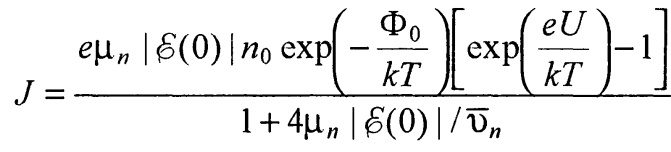 (50)
(50)
Если максимальная напряженность электрического поля в запорном слое настолько мала, что 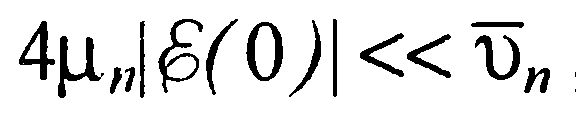 , то в знаменателе выражения (50) вторым членом можно пренебречь. Например, для кремния при Г =300 К это неравенство выполняется, когда
, то в знаменателе выражения (50) вторым членом можно пренебречь. Например, для кремния при Г =300 К это неравенство выполняется, когда 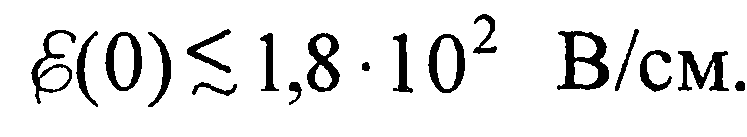 Поскольку
Поскольку 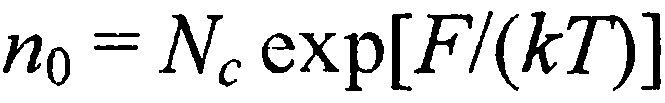 , то выражение для вольтамперной характеристики запорного слоя при выполнении записанного выше неравенства можно представить в следующем виде:
, то выражение для вольтамперной характеристики запорного слоя при выполнении записанного выше неравенства можно представить в следующем виде:
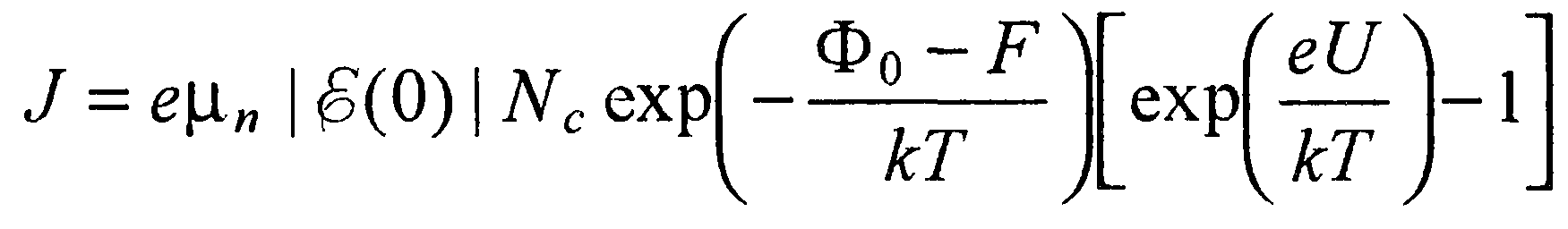 (51)
(51)
Из соотношений (44) и (24) видно, что
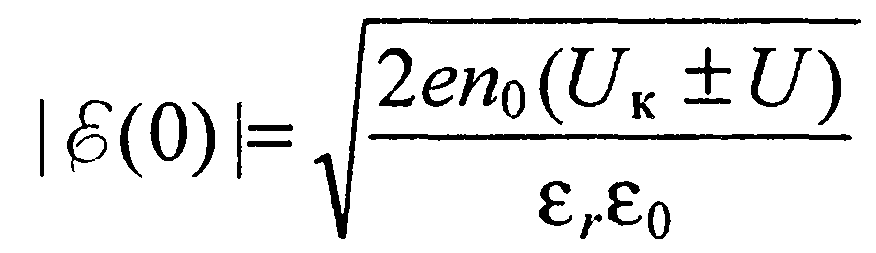 (52)
(52)
Следовательно, плотность прямого тока по диффузионной теории при U > 2,3 кТ/е
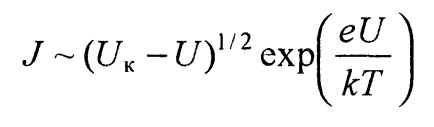 (53)
(53)
должна увеличиваться с ростом напряжения слабее, чем по диодной теории. Плотность обратного тока при |U| > 2,3 кТ/е
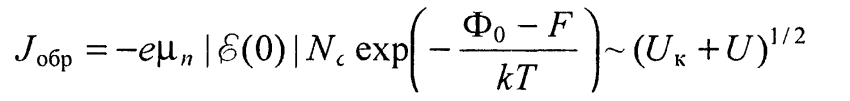 (54)
(54)
слабо растет при увеличении U.
Теперь сравним по величине плотность обратного тока по диодной теории, которую с учетом соотношения (38) можно записать в виде
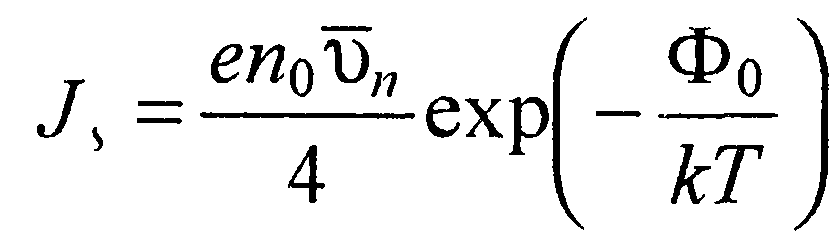 (55)
(55)
с плотностью обратного тока по диффузионной теории
 (56)
(56)
Поскольку 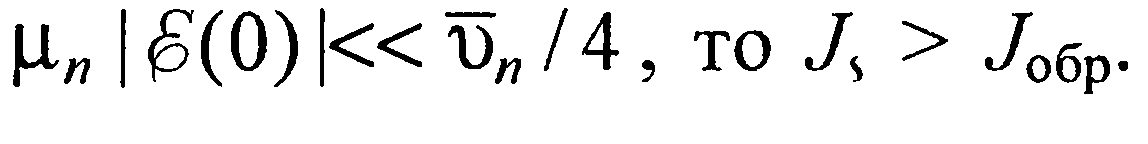 Ясно, что и прямой ток при фиксированных значениях напряжения по диффузионной теории меньше, чем по диодной. При
Ясно, что и прямой ток при фиксированных значениях напряжения по диффузионной теории меньше, чем по диодной. При 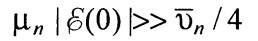 соотношение (50) описывает плотность тока по диодной теории.
соотношение (50) описывает плотность тока по диодной теории.
Из рассмотренного материала видно, что контакт металл - полупроводник с запорным слоем Шоттки обладает резко асимметричной вольтамперной характеристикой и, следовательно, может быть использован для выпрямления переменного тока. Полупроводниковые диоды, в основе действия которых лежат функциональные возможности запорного слоя Шоттки, получили название диодов с барьером Шоттки.
