Глава 2. дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка, допускающие понижение порядка
Основные понятия
Определение 1.Уравнение вида:
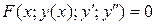 (1)
(1)
называется дифференциальным уравнением второго порядка. Если из этого уравнения выразить

то оно называется разрешенным относительно второй производной.
Определение 2.Общим решением уравнения (1) называется семейство функций, зависящее от двух произвольных постоянных  и
и 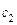 :
:

или 
В первом случае его называют общим решением, во втором – общим интегралом уравнения (1).
Определение 3.Задачей Коши для уравнения (1) и заданных начальных условий: 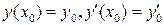 называется поиск частного решения этого уравнения, удовлетворяющего этим начальным условиям:
называется поиск частного решения этого уравнения, удовлетворяющего этим начальным условиям:

где 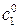 и
и  определенные числа, полученные из общего решения при подстановке в него начальных условий.
определенные числа, полученные из общего решения при подстановке в него начальных условий.
Уравнения второго порядка, допускающие понижение порядка
1) Уравнение не содержит явно 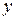 и
и 
Пусть дифференциальное уравнение второго порядка имеет вид:
 (2)
(2)
Тогда, учитывая равенство:  получим:
получим:

Следовательно, общее решение уравнения (2) задается функцией:

2) Уравнение не содержит явно 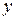
Пусть уравнение (1) имеет вид:
 (3)
(3)
Для решения такого уравнения выполняется замена:

Эта замена понижает порядок уравнения, приводя уравнение (3) к ДУ первого порядка:

Решим полученное уравнение относительно функции 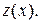 Получим общее решение этого уравнения:
Получим общее решение этого уравнения:

где 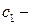 произвольная постоянная.
произвольная постоянная.
Далее, подставив в полученное решение  получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:

Откуда получим:
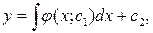
где  произвольная постоянная.
произвольная постоянная.
Итак, получено общее решение уравнения (3):

3) Уравнение не содержит явно 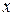
Пусть уравнение (1) имеет вид:
 (4)
(4)
Для решения такого уравнения выполняется замена:

Эта замена понижает порядок уравнения, приводя уравнение (4) к ДУ первого порядка:

Решим полученное уравнение относительно функции 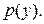 Получим общее решение этого уравнения:
Получим общее решение этого уравнения:

где 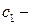 произвольная постоянная. Далее, подставив в полученное решение
произвольная постоянная. Далее, подставив в полученное решение  получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:

Это уравнение с разделяющимися переменными:

где  произвольная постоянная.
произвольная постоянная.
Итак, получим общий интеграл уравнения (4):
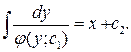
Примеры с решениями
Пример 1. Решить уравнение:

Решение. Это уравнение не содержит 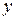 и
и 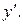 Учитывая равенство
Учитывая равенство  получим
получим
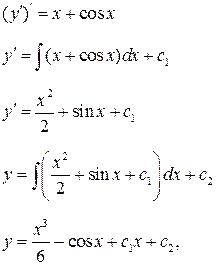
где  и
и  произвольные постоянные.
произвольные постоянные.
Ответ: 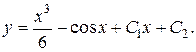
Пример 2. Решить уравнение:

Решение. Это уравнение не содержит явно 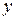 . Поэтому выполним замену:
. Поэтому выполним замену:

Такая замена понижает порядок данного уравнения и приводит к уравнению первого порядка:

Это уравнение является однородным первого порядка вида  так как:
так как:

Выполним замену:

Тогда получим:
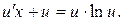 (*)
(*)
Уравнение получилось с разделяющимися переменными. Получим его решение, разделяя переменные, а затем интегрируя:


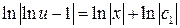
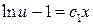

Получили общее решение уравнения (*). Вернемся к переменным 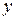 и
и 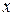 :
:

Подставив  в общее решение, получим дифференциальное уравнение первого порядка:
в общее решение, получим дифференциальное уравнение первого порядка:


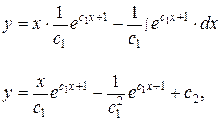
где 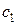 и
и 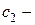 произвольные постоянные.
произвольные постоянные.
Получили общее решение данного уравнения.
Ответ: 
Пример 3. Решить уравнение:
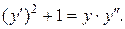
Решение. Это уравнение не содержит явно 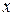 . Поэтому выполним замену:
. Поэтому выполним замену:
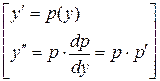
Такая замена понижает порядок данного уравнения и приводит к дифференциальному уравнению первого порядка:
 (**)
(**)
Это уравнение является уравнением с разделяющимися переменными, так как:

Получим его решение, разделяя переменные, а затем интегрируя:
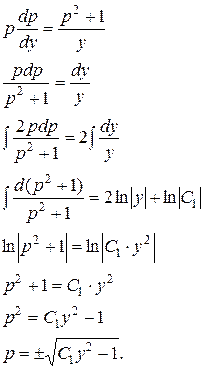
Получили общее решение уравнения (**). Вернемся к переменным 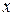 и
и 
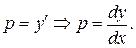
Подставив  в полученное решение, получим дифференциальное уравнение первого порядка c разделяющимися переменными:
в полученное решение, получим дифференциальное уравнение первого порядка c разделяющимися переменными:

где  и
и  произвольные постоянные.
произвольные постоянные.
Получили общий интеграл данного уравнения.
Ответ: 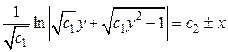 .
.
Пример 4. Решить задачу Коши:


Решение. Данное уравнение не содержит явно 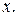 Поэтому выполним замену:
Поэтому выполним замену:
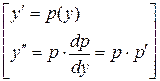
Такая замена приводит к дифференциальному уравнению первого порядка:

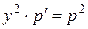 (***)
(***)
Получили уравнение с разделяющимися переменными. Решим его, разделяя переменные, а затем интегрируя:


Получили общее решение уравнения (***). Вернемся к переменным 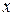 и
и 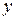 :
:
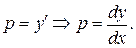
Подставив  в полученное решение, получим дифференциальное уравнение первого порядка с разделяющимися переменными:
в полученное решение, получим дифференциальное уравнение первого порядка с разделяющимися переменными:

где  и
и  произвольные постоянные.
произвольные постоянные.
Получили общий интеграл данного уравнения. Используем начальные условия: 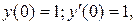 чтобы найти значения
чтобы найти значения  и
и  для частного решения данного уравнения.
для частного решения данного уравнения.

Следовательно, решением задачи Коши является частное решение уравнения, получающееся из общего при подстановке в него значений  и
и 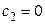 :
:

Ответ: 
Примеры
Решить уравнения или задачи Коши:
1. 
2. 
3. 
4. 
5. 
6. 
7. 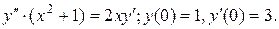
8. 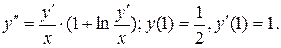
9. 
10. 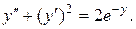
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Ответы
1. 
2. 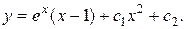
3. 
4. 
5. 
(или 
6. 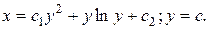
7. 
8. 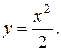
9. 
10. 
11. 
12. 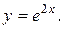
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Замечание. Дифференциальные уравнения вида 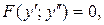 не содержащие в явном виде как независимую переменную
не содержащие в явном виде как независимую переменную  так и искомую функцию
так и искомую функцию  можно решать как уравнение вида 2) или 3).
можно решать как уравнение вида 2) или 3).
