Теорія и методика навчання математики у вищій та середній школі
1. Натуральні числа. Читання та запис Системи числення. Алгоритми дій над натуральними числами в різних системах числення. Розв'язання арифметичних задач. Теорія подільності натуральних чисел. Теорія числа, складені числа. Основна теорема арифметики. НСД, НСК. Ділення і з остачею.
2. Вирази із змінними. Тотожньо рівні вирази. Тотожності. Тотожні перетворення та їх види.
3. Рівняння. Рівносильність рівнянь. Системи рівнянь. Розв'язування рівнянь та систем рівнянь. Раціональні рівняння.
4. Ірраціональні рівняння. Системи ірраціональних рівнянь. Розв'язування ірраціональних рівнянь та систем ірраціональних рівнянь. Розв'язування задач на складання рівнянь.
5. Показникові та логарифмічні рівняння, методи їх розв'язування.
6. Нерівності. Раціональні нерівності. Метод і інтервалів. Ірраціональні нерівності, логарифмічні та показникові нерівності. Функції 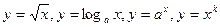 .
.
7. Тригонометричні функції. Різні способи їх введення: аксіоматичний, аналітичний і т.д. ( sin x, cos x - як функції, задані нескінченим рядом; як розв'язок диференціальних рівнянь). Обернені тригонометричні функції.
8. Тригонометричні рівняння та їх розв'язування.
9. Тригонометричні нерівності та їх розв'язування.
10. Елементарні функції та їх властивості. Алгебра графіків функцій.
11. Композиція функцій та їх графіків. Побудова графіків функцій.
12. Геометрія. Планіметрія. Основні поняття геометри. Аксіоми. Основні теореми планіметрії. Методи розв'язування задач з планіметри.
13. Геометричні перетворення площини. Застосування геометричних перетворень площини до розв'язування задач на доведення та побудову.
14. Вектори. Застосування векторів до розв'язування задач з планіметрії.
15. Побудова зображень просторових фігур.
16. Побудова перерізів многогранників та тіл обертання.
17. Площі поверхонь та об'єм многогранників та тіл обертання.
18. Предмет методики математики. Методи методики математики. Зв'язок методики математики з іншими науками. Мета навчання математиці в школі. Провідні ідеї шкільного курсу математики.
19. Методи викладання математики. Поняття методу викладання. Проблема класифікації методів. Репродуктивні методи : лекція, алгоритмічний метод., програмоване навчання.
20. Евристичні методи: метод доцільних задач, евристична бесіда, проблемний метод, практичні роботи, самостійна робота. Індукція та дедукція. Аналіз та синтез. Аналогія.
21. Організація математичного апарату. Методика вивчення понять. Математичні поняття. Зв'язок між поняттями. Означення понять (класичне, генетичне, через абстракцію).
22. Методика вивчення теорем. Структура теорем. Необхідні, достатні, необхідні та достатні умови. Спосіб доведення від супротивного. Етапи роботи над засвоєнням теореми.
23. Розвиток поняття про число в середній школі. Різні схеми вивчення числових множин. Натуральні числа. Узагальнення та систематизація знань про запис та читання натуральних чисел, про дії та закони дій над натуральними числами. Подільність. Використання дидактичних ігор.
24. Додатні раціональні числа. Методика введення і раціональних чисел. Дії над раціональними числами. Проценти. Розв'язування задач.
25. Введення поняття про від'ємні числа. Дії вад раціональними числами. Поняття про дійсні числа. Дії над наближеними числами.
26. Методика вивчення тотожних перетворень в школі. Формування поняття про числовий вираз та вираз із змінною. Класифікація виразів. Різні точки зору на тотожні перетворення. Перетворення раціональних та ірраціональних виразів.
27. Основні поняття лінії рівнянь та нерівностей. Про трактовку поняття рівняння. Рівносильність та логічне слідування. Основні методи розв'язування рівнянь та нерівностей. Етапи вивчення рівнянь та нерівностей в школі.
28. Вивчення функцій в шкільному курсі математики. Поняття про функцію. Введення функції. Степенева функція. Лінійна функція. Квадратична функція.
29. Методика вивчення показникової функції. Узагальнення поняття степеня. Введення показникової функції. Основні прийоми розв'язування і показникових рівнянь та нерівностей.
30. Логарифмічна функція як обернена до показникової. Методика розв'язування логарифмічних рівнянь та нерівностей.
31. Тригонометричні функції в курсі математики середньої школи. Етапи вивчення тригонометричних функцій. Введення радіанної міри кута. Означення тригонометричних функцій числовою аргументу. Властивості тригонометричних функцій. Обернеш тригонометричні функції. Тригонометричні рівняння та нерівності.
32. Елементи інтегрального та диференціального числення в шкільному курсі математики. Різні формулювання означення похідної та задачі, що до нього підводять. Методика вивчення застосування похідної до дослідження функцій Методика вивчення елементів інтегрального числення. Введення первісної. Застосування, інтеграла до обчислення площ фігур. Визначений інтеграл.
33. Структура шкільного курсу геометрії. Ступені вивчення геометри в школі. Основні ідеї курсу геометрії. Логічна будова курсу геометрії.
34. Методика проведення перших уроків. Робота над поняттями. Основні компоненти роботи над | теоремою. Метод рівних трикутників та його використання.
35. Методика розв'язування задач на побудову. Значення і місце теми. Позиційні та непозиційні задачі. Схема розв'язування задач на побудову. Методи розв'язування конструктивних задач в планіметрії.
36. Стереометричні задачі на побудову. Зображення і просторових фігур на площині. Задачі на і побудову: моделювання, уявні побудови, побудови на проекційному малюнку. Використання побудов при розв'язуванні і стереометричних задач.
37. Перетворення на площині. Що таке перетворення ? Схема вивчення рухів. Рухи і рівність фігур.
38. Методика розв'язування задач на доведення з використанням рухів. Значення геометричних перетворень при розв'язуванні задач. Використання осьової та центральної симетрії. Особливості задач, що розв'язуються з допомогою повороту площини. Використання паралельного перенесення при розв'язуванні задач.
39. Методика вивчення подібності фігур. Значення теми. Схема вивчення перетворення подібності. і Використання подібності в інших розділах геометрії. Ключові задачі.
40. Метод координат в шкільній математиці. Координати як предмет вивчення та як метод викладання математики. Схема вивчення координатного методу. Методика розв'язування задач координатним методом.
41. Вектори. Методика їх вивчення в школі. Значення і місце теми. Означення поняття вектора. Операції над векторами. Навчання розв'язуванню задач векторним методом.
42. Методика вивчення величин. Поняття величини. Вимірювання величин. Довжина відрізка. Периметр. Довжина кола.
43. Площа фігури та її вивчення. Площа. Площа прямокутника. Площа многокутників. Площа круга. Площі поверхонь многогранника, конуса, циліндра, сфери.
44. Вивчення об'ємів тіл. Об'єм прямокутного паралелепіпеда. Об'єм піраміди. Об'єм кулі.
45. Взаємне розміщення прямих і площин в просторі. Про послідовність вивчення взаємного розміщення прямих і площин в просторі. Паралельність прямих і площин. Перпендикулярність в просторі.
46. Методика вивчення многогранників. Особливості вивчення теми. Означення многогранники. Класифікація многогранників. Центральні многогранники.
47. Тіла обертання. Фігура і тіло. Циліндр. Конус. Куля. Розв’язання задач на комбінацію фігур.
Математичний аналіз
Вступ до аналізу
Математичні величини, сталі, та змінні величини. Елементарна та вища математика, їх об’єкти дослідження. Функціональні залежності між математичними величинами. Предмет і метод математичного аналізу. Зв’язок математичного аналізу з шкільним курсом математики.
Числові множини N, Z, Q. Операції над раціональними числами. Властивості раціональних чисел. Множина ірраціональних чисел. Аксіома Кантора. Властивості ірраціональних чисел. Множина дійсних чисел. Основні властивості дійсних чисел. Скінченні та нескінченні числові проміжки. Принцип вкладених відрізків.
Модуль дійсного числа. Властивості модуля дійсного числа. Розв’язування рівнянь та нерівностей за допомогою персонального комп’ютера.
Поняття околу точки числової прямої. Обмежені числові множини. Точна верхня і точна нижня межи числової множини. Принцип Вейерштрасса.
Задачі, які приводять до поняття функції. Поняття відповідності та функції. Область визначення та множина значень функції. Звуження та розширення функції. Способи завдання функції. Обернена функція, графіки взаємо-обернених функцій. Композиція функцій. Арифметичні операції над функціями.
Класифікація функцій: обмежені та необмежені функції, монотонні функції, парні та непарні функції, періодичні функції. Основні елементарні функції. Елементарні функції: цілі раціональні функції; дробово-раціональні функції; ірраціональні функції; алгебраїчні та трансцендентні функції. Побудова графіків елементарних функцій, елементарні перетворення графіків функцій, побудова графіків функцій за допомогою персонального комп’ютера.
Означення та способи завдання числової послідовності. Монотонні числові послідовності. Обмежені числові послідовності. Арифметичні операції над числовими послідовностями. Границя числової послідовності. Збіжні та розбіжні послідовності. Найпростіші теореми про границі. Фундаментальні послідовності. Критерій Коші збіжності послідовності.
Нескінченно малі та нескінченно великі числові послідовності, їх властивості. Основні властивості границь: зв’язок збіжної послідовності з нескінченно малою числовою послідовністю, границя суми, добутку, частки, різниці числових послідовностей. Існування границі монотонної обмеженої послідовності.
Означення границі функції в точці та на нескінченності по Коші та Гейне. Критерій існування границі функції. Теореми про границі. Деякі важливі границі. Обчислення границь числових послідовностей та функцій в точці за допомогою персонального комп’ютера.
Односторонні границі функції в точці. Нескінченно малі функції. Еквівалентні нескінченно малі функції. Нескінченно малі функції різних порядків. Нескінченно великі функції. Теореми про границі.
Задачі, які приводять до поняття неперервності функції. Неперервність функції в точці. Критерій неперервності функції в точці. Арифметичні дії над неперервними функціями. Неперервність функції на множині. Неперервність основних елементарних та елементарних функцій. Неперервність складної функції. Точки розриву функції І і ІІ роду.
Властивості функцій неперервних на відрізку. Рівномірна неперервність, теорема Кантора.
Диференціальне числення функції однієї змінної
Задачі, які приводять до поняття похідної. Означення похідної функції дійсної змінної. Геометричний та механічний зміст похідної.
Поняття функції диференційованої у точці і на множині. Зв’язок диференційованості з неперервністю. Основні правила диференціювання функції: похідна суми, добутку і частки; похідна складної функції; похідна оберненої функції. Похідні елементарних функцій. Диференціювання параметрично і неявно заданих функцій.
Диференціал функції, його геометричний і механічний зміст. Інваріантність форми диференціала. Застосування диференціала до наближених обчислень. Похідні і диференціали вищих порядків.
Основні теореми про диференційовані функції на відрізку: теорема Ролля, Лагранжа, Коші; формула Тейлора; правило Лопіталя.
Дослідження функцій за допомогою похідних. Зростання та спадання функцій. Критичні точки. Необхідна і достатні умови локального екстремуму функції. Знаходження найбільшого і найменшого значень функції на відрізку.
Опуклість і вгнутість кривої, точки перегину. Асимптоти кривих. Загальна схема дослідження функцій та побудова її графіків.
Аналіз графіків функцій які побудовано за допомогою персонального комп’ютера.
Інтегральне числення функцій однієї змінної
Задачі, які приводять до поняття первісної. Первісна у шкільному курсі математики. Поняття первісної, теорема про множину первісних. Поняття неозначеного інтеграла. Властивості неозначеного інтеграла. Таблиця основних інтегралів.
Основні методи інтегрування функцій: метод розкладу, метод підстановки, метод інтегрування за частинами.
Інтегрування елементарних раціональних дробів. Інтегрування раціональних функцій. Інтегрування деяких класів ірраціональних функцій. Інтегрування трансцендентних функцій (тригонометричних, обернених тригонометричних, гіперболічних, логарифмічних та показникових). Інтегрування функцій за допомогою персонального комп’ютера.
Задачі, які приводять до поняття означеного інтеграла. Означений інтеграл. Інтегрованість функції за Ріманом. Необхідна умова інтегрованості.
Суми Дарбу та їх властивості. Критерій інтегрованості функції за Ріманом. Класи інтегрованих функцій (інтегрованість неперервної функції на відрізку, інтегрованість монотонної функції, інтегрованість обмеженої кусково-неперервної функції). Властивості означеного інтеграла.
Означений інтеграл із змінною верхньою межею інтегрування. Формула Н’ютона – Лейбніца. Формула зміни змінної і інтегрування за частинами для означеного інтеграла.
Наближені обчислення означених інтегралів: постановка задачі, формула прямокутників, формула трапецій, параболічна формула. Обчислення означених інтегралів за допомогою персонального комп’ютера.
Невласні інтеграли з нескінченними границями і невласні інтеграли від необмежених функцій. Ознаки збіжності невласних інтегралів.
Застосування означеного інтеграла до обчислення площ плоских областей (випадки декартової та полярної систем координат, параметрично заданої кривої)
Застосування означеного інтеграла до обчислення об’єму тіла обертання.
Поняття спрямлюваної кривої. Критерій спрямлюваності. Адитивна властивість спрямлюваної кривої. Обчислення довжин кусково-гладких кривих. Диференціал довжини дуги. Кривина і радіус кривини дуги.
Застосування означеного інтеграла до обчислення площі поверхні обертання.
Використання персонального комп’ютера при обчисленні площ плоских фігур, об’ємів та поверхонь тіл обертання.
Застосування означеного інтеграла у фізиці (обчислення центру ваги кривої, центру ваги криволінійної трапеції, статичних моментів, механічної роботи та сили тиску).
Числові та функціональні ряди
Числові ряди. Місце і значення розділу “Ряди” у курсі математичного аналізу. Основні поняття щодо числових рядів. Геометричний та гармонічний ряди.
Необхідна ознака збіжності числового ряду. Дії над рядами: додавання рядів, множення ряду на число. Критерій Больцано – Коші збіжності числового ряду. Ознаки порівняння.
Достатні ознаки збіжності числових рядів: Даламбера, Коші (радикальний та інтегральний).
Знакозмінні числові ряди. Абсолютна та умовна збіжність рядів. Ознака Лейбніца та її застосування.
Степеневі ряди. Теорема Абеля. Радіус збіжності. Рівномірна збіжність. Інтегрування та диференціювання степеневих рядів.
Розклад функції в ряди Тейлора та Макларена. Степеневі ряди для функцій: sinx, cosx, ex, ln(1+x), (1+x)a.
Степеневі ряди з комплексними членами. Застосування степеневих рядів до наближених обчислень: значень функцій, інтегралів тощо.
Функціональні послідовності, їх збіжність, рівномірна збіжність.
Функціональний ряд, його збіжність, рівномірна збіжність. Критерій збіжності функціонального ряду.
Властивості рівномірної збіжності функціональних послідовностей і рядів.
Лінійна алгебра
Системи лінійних рівнянь
Системи лінійних рівнянь, основні означення. Матриця системи лінійних рівнянь. Перетворення системи у процесі розв’язування. Лінійні комбінації. Лінійні перетворення систем. Перетворення системи лінійних рівнянь методом Гаусса. Аналіз вивідної системи лінійних рівнянь. Знаходження розв’язків системи лінійних рівнянь.
Матриці і визначники
Перестановки. Властивості інверсій. Транспозиції. Подвійні перестановки. Означення детермінанта n-го порядку. Обчислення детермінантів другого та третього порядків. Основні властивості детермінантів. Рівноправність рядків і стовпців детермінанта. Означення мінорів і алгебраїчних доповнень. Розкладання детермінанта за елементами рядка або стовпця. Інші властивості алгебраїчних доповнень. Теорема Лапласа. Добуток детермінантів. Способи обчислення детермінантів n-го порядку. Детермінант Ван дер Монда. Розв’язування систем лінійних рівнянь за допомогою детермінантів. Означення операцій над матрицями. Властивості операцій над матрицями. Обернена матриця. Методи обчислення оберненої матриці. Кільце квадратних матриць.
Векторні простори
Означення векторного простору. Найпростіші наслідки з аксіом векторного простору. Лінійна залежність векторів. Розмірність векторного простору. Базис векторного простору. Координати вектора. Зв’язок між базисами. Перетворення координат вектора. Ізоморфізм векторних просторів. Підпростори векторного простору. Лінійні оболонки. Лінійний многовид. Перетин і сума підпросторів. Означення евклідового простору. Довжина вектора. Кут між векторами. Ортогональний базис. Ортонормований базис. Ізоморфізм евклідових просторів. Ортогональне доповнення підпростору. Простір розв’язків лінійної однорідної системи рівнянь. Фундаментальна система розв’язків лінійної однорідної системи рівнянь. Лінійний многовид розв’язків лінійної неоднорідної системи рівнянь.
Лінійні оператори
Означення і найпростіші властивості лінійних операторів. Завдання лінійного оператора за допомогою відображення базису. Матриця лінійного оператора. Зв’язок між матрицями лінійного оператора в різних базисах. Подібні матриці. Операції над лінійними операторами та їх властивості. Лінійні алгебри. Ізоморфізм лінійних алгебр. Ранг і дефект лінійного оператора. Вироджені оператори. Обернений оператор. Повна лінійна група. Інваріантні підпростори. Власні вектори й власні значення лінійного оператора. Характеристичне рівняння лінійного оператора. Лінійні оператори з простим спектром. Зведення матриці до діагонального виду. Симетричні оператори. Квадратичні форми в дійсному евклідовому просторі.
Системи лінійних нерівностей
Системи лінійних нерівностей, їх геометричний смисл. Однорідні системи лінійних нерівностей. Критерій несумісності системи. Невід’ємні розв’язки системи лінійних нерівностей. Графічний спосіб розв’язування систем лінійних нерівностей. Задачі лінійного програмування, їх математичне формулювання, геометрична інтерпретація та різні форми завдання. Геометричний спосіб розв’язування. Симплекс-метод.
Аналітична геометрія
Елементи векторної алгебри
Вступ. Вектор (поняття). Додавання, віднімання векторів, множення вектора на число, ділення колінеарних векторів та їх властивості. Скалярний добуток векторів та його властивості. Лінійна комбінація та лінійна залежність векторів. Координати вектора відносно даного базису та їх властивості.
Метод координат на площині
Афінна система координат на площині; прямокутна декартова система координат. Ділення відрізка в даному відношенні; віддаль між двома точками на площині. Полярні координати; перехід від полярних координат до декартових і навпаки. Геометричне тлумачення рівнянь та нерівностей між координатами. Пряма лінія. Різні способи задання прямої на площині; різні види рівнянь прямої в афінній системі координат. Геометричний смисл знака тричлена Ax+By+C . Пряма лінія в прямокутній системі координат; нормальне рівняння прямої. Віддаль від точки до прямої. Кут між прямими. Пучок прямих.
Перетворення площин та їх застосування
до розв’язування задач елементарної геометрії
Відображення, геометричні перетворення (основні поняття). Афінні перетворення: поняття, інваріанти. Група афінних перетворень. Перетворення подібності як окремий випадок афінного перетворення. Власно-подібне та дзеркально-подібне перетворення. Група перетворень подібності. Гомотетія як окремий випадок афінного перетворення. Рухи як окремий випадок перетворення подібності. Класифікація рухів. Група рухів. Рухи першого роду: перенос, поворот навколо точки, центральна симетрія. Рухи другого роду: осьова симетрія. Стиск до прямої. Перетворення подібності, відмінні від рухів та гомотетії. Інверсія: поняття інверсії прямої та кола. Ерлангенська програма Ф. Клейна.
Лінії другого порядку
Еліпс: поняття, канонічне рівняння, властивості. Еліпс як афінний образ кола. Гіпербола: поняття, канонічне рівняння, властивості. Парабола: поняття, канонічне рівняння, властивості. Лінії другого порядку як конічні перерізи. Рівняння ліній другого порядку в полярних координатах. Загальне рівняння ліній другого порядку та зведення його до канонічного виду методом геометричних перетворень. Центр лінії другого порядку. Діаметри, вісі, дотичні ліній другого порядку. Асимптотичні напрямки, асимптоти.
Метод координат у тривимірному просторі
Афінна та декартова системи координат у просторі. Ділення відрізка в даному відношенні. Віддаль між двома точками. Векторний та мішаний добутки векторів та їх застосування.
Площини та прямі
Площина: різні способи задання площини, рівняння площини. Взаємне розташування площин. Пучок та в’язка площин. Різні способи задання прямої у просторі; рівняння прямої. Взаємне розташування двох прямих у просторі. Взаємне розташування прямої і площини. Кути між прямими, між прямою і площиною. Геометричний смисл знака многочлена Аx+By+Cz+D. Площина в прямокутній системі координат.
Випуклі многогранники
Випуклі многогранники. Теорема Ейлера. Правильні многогранники.
Вивчення поверхонь другого порядку канонічними рівняннями
Поверхні обертання, поверхні другого порядку. Еліпсоїд, гіперболоїди та параболоїди. Циліндричні та конічні поверхні другого порядку. Прямолінійні твірні гіперболоїдів та параболоїдів.
Афінний та евклідів n-вимірні простори
n-вимірний афінний простір. Ізоморфізм усіх n-вимірних афінних просторів. Пряма та площина в n-вимірному афінному просторі. N-вимірний евклідів простір.
Квадратичні форми і квадрики
Квадратичні форми, зведення їх до канонічного виду. Квадрики поверхні другого порядку. Дотична площина. Центр поверхні другого порядку. Діаметральна площина. Голововні напрямки. Властивості розв’язків характеристичного рівняння. Перетворення рівняння поверхні другого порядку.
Проективний простір
Поняття проективного простору. Однорідні афінні координати. Рівняння прямої на площині в однорідних координатах. Координати прямої на площині. Принцип двоїстості. Теорема Дезарга. Конфігурація Дезарга. Просте та складне відношення точок прямої. Проективні координати на прямій. Просте та складне відношення прямих пучка. Проективні форми. Координатне представлення проективної відповідності. Проективні координати на площині. Перетворення проективних координат. Аналітичне представлення проективних перетворень площини. Гармонічна четвірка точок. Повні чотиривершинник та чотирибічник. Інволюція. Поляра точки відносно лінії. Полюс лінії 2-го порядку. Теорема Паскаля та Бріаншона.
Геометричні побудови на площині
Система постулатів побудов за допомогою циркуля та лінійки. Основні задачі на побудову. Різні методи геометричних побудов на площині. Метод геометричних перетворень (Рухи). Методи подібності та гомотетії в геометричних побудовах. Алгебраїчний метод розв’язування задач на побудову. Приклади класичних задач на побудову, що не розв’язуються циркулем та лінійкою. Побудови Штейнера та Маскероні.
Методи зображень
Різні види проектування на площину: паралельне, ортогональне, центральне. Метод Монжа. Аксонометрія. Зображення плоских фігур. Зображення просторових фігур. Теорема Полька-Шварца. Побудова перерізів геометричних фігур. Побудова зображень і афінна система координат. Паралельна аксонометрія.
Основи геометрії
Геометрія до Евкліда. Начала Евкліда. Теорія паралельних прямих у Евкліда. Виникнення проблеми п’ятого постулату та невдалі спроби його доведення. Аксіоматичне обґрунтування геометрії. Система аксіом Гільберта (огляд). Аксіома паралельності. Абсолютна геометрія. Неевклідова геометрія паралельних. М.І.Лобачевський та його геометрія. Кут паралельності. Функція Лобачевського. Криві сталої кривини: коло, еквідістанта. Інтерпретації геометрії Лобачевського. Елементи сферичної геометрії. Еліптична геометрія Рімана.
Задача вимірювання геометричних величин
Вимірювання довжини. Вимірювання площ та об’ємів.
Лінії і поверхні в евклідовому просторі. Елементи топології
Неперервні відображення підмножин евклідового простору. Гомеоморфізм. Поняття кривої. Гладкі криві. Способи задання. Векторна функція скалярного аргументу. Дотична пряма до кривої. Стична площина кривої. Довжина дуги кривої. Натуральна параметризація кривої. Кривина і скрут кривої. Натуральні рівняння кривої. Поняття поверхні. Гладкі поверхні, способи задання. Дотична площина поверхні. Нормаль. Довжина дуги. Кут між кривими. Площа поверхні. Кривина кривої на поверхні. Теорема Меньє. Індикатриса Дюпена. Характеристичне рівняння поверхні. Повна та середня кривина. Внутрішня геометрія поверхні. Поняття про вигинання поверхні. Теореми Гауса. Дефект геодезичного трикутника.
Історія математики
Зародження математики і період практичної математики
Утворення математичних уявлень в первісному суспільстві. Виникнення поняття натурального числа. Різні системи усної та письмової нумерації. Основні математичні знання народів стародавніх цивілізації Єгипту і Шумеро-Вавілонії.
Створення теоретичної математики
Математика в країнах греко-римської культури з VI ст. до н.е. до V ст. н.е. Перетворення математики в абстрактну дедуктивну науку. Піфагорійська математика. Перша криза методологічних основ математики і її подалання. Перші математичні теорії.
Елементарна математика
Математика країн Близького і Середнього Сходу та Європи. Математика епохи Відродження.
Створення математики змінних величин
Поява змінних величин в математиці. Створення аналізу нескінченно малих. Друга криза методологічних основ математики. формування комплексу дисциплін класичної вищої математики: аналітичної, нарисної, проективної, афінної, диференціальної геометрії; теорії ймовірностей.
Сучасна математика
Розвиток математичного аналізу. Арифметизація класичного аналізу і створення дійсних чисел. Початки теорії функції дійсної змінної. Відкриття неевклідової геометрії. Інтерпретація нових геометричних систем. Аксіоматична побудова математики. Алгебра ХІХ ст. Проблема розв’язання в радикалах алгебраїчних рівнянь степеня вище 4-го. Теорія груп і її значення. Формування нового погляду на алгебру, як на теорію алгебраїчних структур. Математика на рубежі ХІХ-ХХ ст.: народження нових дисциплін (функціонального аналізу, топології). Математизація інших наук та практики в ХІХ і ХХ ст. Поява нових галузей математичної науки.
Внесок в розвиток математики провідних українських вчених.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Александров П.С. Курс аналитической геометрии. М., Наука, 1979.
2. Алгебра и теория чисел.: Учеб. Пособие для студентов-заочников 2 курса физ.-мат. Фак. пед. институтов (Н.А. казачек, Г.Н. Перлатов и др.); Под ред. Н.Я. Виленкина. - 2-е издание М.: Просвещение, 1984. -192с.
3. Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу: Учебник для университетов и пед.вузов. – М.: Высшая школа, 2000. – 695с.
4. Атанасян Л.С. Геометрия. М., Просвещение, 1973.
5. Атанасян Л.С., Гуревич Г.Б. Геометрия. М., Просвещение, 1976, ч. ІІ.
6. Атанасян Л.С., Базылев В.Т. Геометрия. М., Просвещение,1986, ч. І, ІІ.
7. Бевз Г.П. Методика викладання математики.-К. :Вища школа, 1985.
8. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1975. – 416с.
9. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 1985. - 383
10. Бородін О.І. Теорія чисел: підручник для пед. інститутів УРСР. – 3-е вид. перероблене і доповнене. – К.: Радянська шк., 1970.-270с.
11. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения. – М.: Высш. шк., 1969. – 366с.
12. Венцель Е.С. Теория вероятностей. – М.: Наука, 1988. – 586с.
13. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся школ и классов с углубленным изучением математики. – 3-е изд. – М.: Просвещение, 1993. – 288с
14. Виленкин Н.Я. Математика. - М.: Просвещение, 1977.
15. Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. Ч. 1-2 – М.: Высшая школа, 2002 - 725
16. Гихман И.И., Сиброход А.А., Ядренко М.И. Теория вероятностей и математическая статистика.. – К.: Вища шк., 1988. - 440с.
17. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Изд.2-е., доп. – М.: Высш. шк., 1975. – 336с.
18. Гмурман В.Е. Теория вероятностей и математическая статистика. Изд. 4-е, доп. Учебное пособие для ВУЗов. – М.: Высш. шк., 1975. – 368с.
19. Дадаян А.А., Дударенко В.А. Алгебра и геометрия: Учеб. Поособие. - Мн.: Высшая шк., 1989. - 213с.
20. Давидов М.О. Курс математичного аналізу. Ч.1-3. – К: Вища школа, 1990, 1991, 1992. – 384, 366, 360с.
21. Давыдов Н.А., Коровкин П.Н., Никольский В.Н. Сборник задач по математическому анализу. – М.: Просвещение, 1973. – 254 с.
22. Данко П.Е. Попов А.К., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1 – 2. М.: Высшая школа, 2001.- 416, 365с.
23. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1990, 624с.
24. Демидович В.П. Задачи и упражнения по математическому анализу. – М., 1968
25. Дороговцев А.Я. Математичний аналіз. частина І-2. – К.: Либідь, 1993,1994.- 20, 304с.
26. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум. -Київ: Вища школа, 1991. - 407 с.
27. Егоров И.П. Геометрия. М., Просвещение, 1979.
28. Жалдак М.І., Кузьміна Н.М., Берлінська С.Ю. Теорія імовірностей і математична статистика з елементами інформаційної технології.: Навч. Посібник. – К.: Вища шк., 1995. - 351с.
29. Завало С.Т., Костарчук В.М., Хацет Б.І. Алгебра і теорія чисел. Ч.2.-К.: Вища школа, 1976.-384с.
30. Завало С.Т., Левіщенко С.С., та ін. Алгебра і теорія чисел. Ч.1. Практикум.-К.: Вища школа, 1983.-232с.
31. Завало С.Т., Левіщенко С.С., та ін. Алгебра і теорія чисел. Ч.2. Практикум.-К.: Вища школа, 1986.-264с.
32. Завало С.Т., Костарчук В.М., Хацет Б.І. Алгебра і теорія чисел. Ч.1.-К.: Вища школа, 1974. –464с.
33. Курош А.Г. Курс высшей алгебры.- М.: Наука, 1975.-431с.
34. Кудрявцев Л.Д. Математический анализ.Т.1-2.- М.: Высшая школа, 1993. – 614 с., 72с.
35. Кушнир И. Шедевры школьной математики. І-П том.-К.,1995.
36. Кушнир И. Методы решения задач по геометрии. - К., 1994.
37. Лавров Й. А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. - М.: Наука, 1975. - 240с.
38. Фихтенгольц Г.М. Основы математического анализа. Т.1-2. – М.: Наука, 1964,1968. – 440с., 437с.
Перелік комп’ютерних програм
1. Gran
2. Mathcad 2000 Professional
