Предел функции в точке и на бесконечности

Рассмотрим функцию 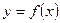, определенную на некотором множестве 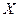и точку 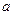, быть может, и не принадлежащую множеству 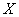, но обладающую тем свойством, что в любой 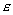–окрестности точки 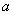имеются точки множества значений аргумента 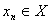, отличные от 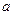. Рассмотрим вопрос о сходимости соответствующей последовательности значений функции .

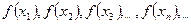Существуют два определения предела функции в точке.

Определение

Число 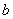называется предельным значением функции 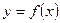в точке 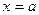(или пределом функции при x® a), если для любой сходящейся к а последовательности 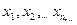значений аргумента 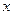, элементы 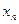которой отличны от 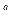, соответствующая последовательность 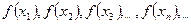значений функции сходится к .

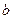Для обозначения предельного значения функции используется следующая символика:

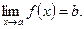
Отметим, что функция 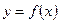может иметь в точке 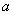только одно предельное значение. Это вытекает из того, что последовательность 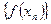может иметь только один предел.

Рассмотрим несколько примеров.

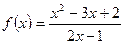
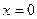1. Функция имеет в точке предел, равный –2. Действительно, пусть 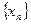– любая последовательность значений аргумента, сходящаяся к нулю, т.е. 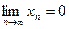, тогда при 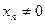в силу теорем о свойствах сходящихся последовательностей:

.

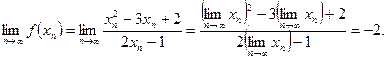2. Функция 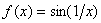определена для всех 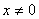. В точке 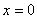эта функция не имеет предела. Для доказательства возьмем две последовательности значений аргумента, сходящиеся к нулю:

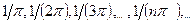и .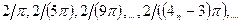

Соответствующие последовательности значений функций для них:

.

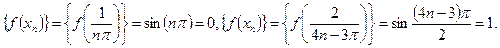Таким образом, Определение 1 не удовлетворяется, так как для двух разных последовательностей значений аргумента, сходящихся к нулю, соответствующие последовательности значений функции имеют разные пределы.

Дадим другое определение пределу функции в точке . Пусть функция определена на некотором интервале , кроме быть может точки .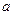

Определение

Число 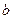называется пределом функции 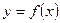в точке 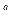, если для любого числа 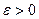существует такое число 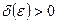, что для всех 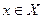, удовлетворяющих условиям 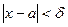при 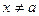, выполняется неравенство .

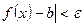Второе определение предела функции означает, что функция 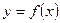имеет предел 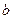в точке 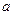, если для любой e–окрестности точки 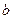можно найти такую d–окрестность точки 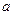, что, как только значение аргумента попадет в эту d–окрестность, соответствующее значение функции 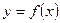будет находиться в e–окрестности точки 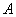(см. рис. 4.3.1).

Рис. 4.3.1

Первое определение предела функции основано на понятии предела числовой последовательности, и его называют определением, «на языке последовательностей» (предел функции по Гейне). Второе определение носит название «на языке d–e» (предел функции по Коши).

Теорема

Первое и второе определения предела функций эквивалентны.

Введем понятия односторонних пределов функции. Дадим определение односторонних пределов функции «на языке d–e».

Пусть функция 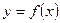определена на полуинтервале 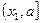(соответственно на полуинтервале 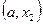, кроме, быть может, точки .

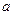Определение

Число b называется правым (левым) пределомфункции в точке а, если для любого 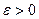существует такое 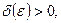, что для всех x из правой (левой) d –окрестности точки а, т.е.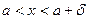 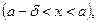выполняется неравенство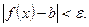

Для правого (левого) предела функции используется символическая запись:

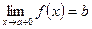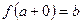
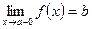
или

или .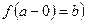

Приведем в качестве примера функцию

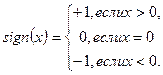
В точке 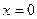эта функция имеет левый и правый пределы:, 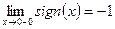, 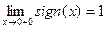. Действительно, для любой сходящейся к нулю последовательности 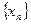, у которой все элементы 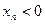, соответствующая последовательность значений функции состоит только из одного числа –1, т.е., предел слева в точке 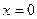также равен этому числу. Аналогично устанавливается и предел справа.

Пример

Найти правый и левый пределы функции .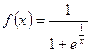

Решение

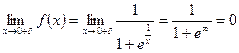– правый предел.

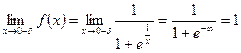– левый предел.

Таким образом видим, что левый и правый пределы не равны!

Теорема

Функция 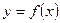имеет в точке а предел тогда и только тогда, когда в этой точке существуют пределы как справа, так и слева, и они равны. В этом случае их общее значение и является двусторонним пределом функции в точке .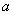