Формулы сокращенного умножения. Ключевые слова: квадрат суммы, квадрат разности, куб суммы, куб разности, разность квадратов, сумма кубов
Ключевые слова: квадрат суммы, квадрат разности, куб суммы, куб разности, разность квадратов, сумма кубов, разность кубов
- Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a+b)2=a2+2ab+b2
- Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй. (a-b)2=a2-2ab+b2
- Произведение суммы двух величин на их разность равно разности их квадратов. (a+b)(a-b)=a2-b2
- Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй. (a+b)3=a3+3a2b+3ab2+b3
- Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй. (a-b)3=a3-3a2b+3ab2-b3
- Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов. ( a+b)(a2-ab+b2)=a3+b3
- Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.(a-b)(a2+ab+b2)=a3- b3
Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения нужно знать наизусть:
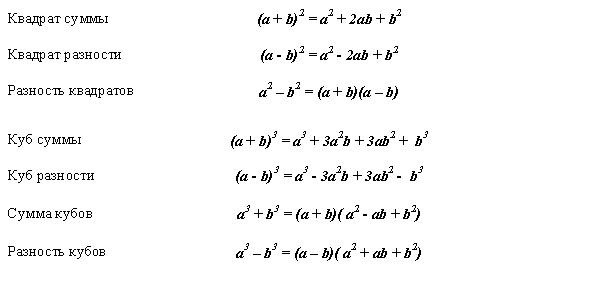
Пример.Докажите формулу a 3 + b 3 = ( a + b )( a 2 – ab + b 2 ).
Решение.Имеем ( a + b )( a 2 – ab + b 2 ) = a 3 – a 2 b + ab 2 + ba 2 – ab 2 – b 3. Приводя подобные слагаемые, мы видим, что ( a + b )( a 2 – ab + b 2 ) = a 3 + b 3, что и доказывает нужную формулу.
Пример. Упростите выражение (2 x 3 – 5 z )(2 x 3 + 5 z ).
Решение. Воспользуемся формулой разности квадратов, получим: (2 x 3 – 5 z )(2 x 3 + 5 z ) = (2 x 3 ) 2 – (5 z ) 2 = 4 x 6 – 25 z 2.
Ответ.4 x 6 – 25 z 2.
Все формулы по теме "Формулы сокращенного умножения"
Формула: 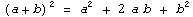 |
Примеры: 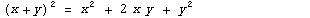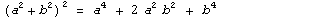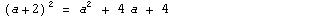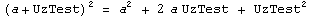 |
Формула: 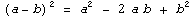 |
Примеры: 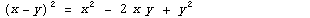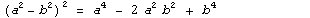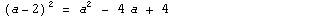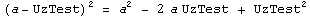 |
Формула: 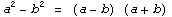 |
Примеры: 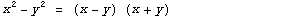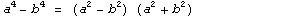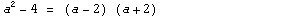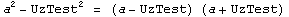 |
Формула: 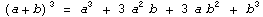 |
Примеры: 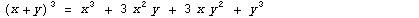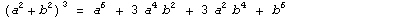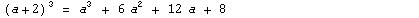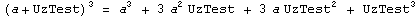 |
Формула: 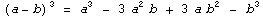 |
Примеры: 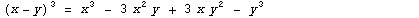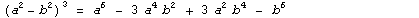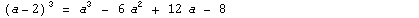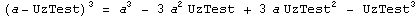 |
Формула: 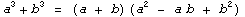 |
Примеры: 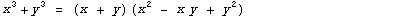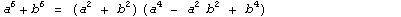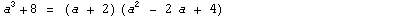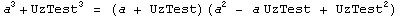 |
Формула: 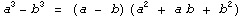 |
Примеры: 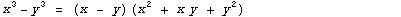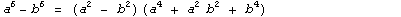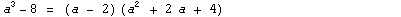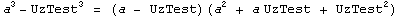 |
Пропорциональность
Пропорция.Равенство a : b = c : d называется пропорцией, если даны четыре отличных от нуля числа a, b, c и d таких, что a : b = c : d. Т.е. пропорция (лат. proportio - соразмерность, выравненность частей) - равенство двух отношений.
Замечание.Числа a и d называются крайними членами пропорции, а числа b и c - средними членами пропорции. Пишут, a : b = c : d , а читают: "a так относится к b, как c относится к d"
Основное свойство пропорции.Произведение крайних членов пропорции равно произведвению средних ее членов.Если ba=cd, то a  d=b
d=b  c
c
Выражение члена пропорции ba=cd через остальные: a=db  c
c  c=ba
c=ba  d
d  b=ca
b=ca  d
d  d=ab
d=ab  c
c
Свойство 1.Если истина пропорция ba=cd, то истины следующие пропорции: ba=db  ab=cd
ab=cd  bd=ca;
bd=ca;
Свойство 2.Если истина пропорция ba=cd, то истины следующие производные пропорции:ba+b=dc+d  ba−b=dc−d
ba−b=dc−d  aa+b=cc+d
aa+b=cc+d  aa−b=cc−d
aa−b=cc−d  a−ba+b=c−dc+d
a−ba+b=c−dc+d
Прямая пропорциональность. Прямая пропорциональность - это функция, заданная формулой y=kx  k
k 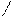 =0 , где k - коэффициент пропорциональности, y и x - пропорциональные переменные
=0 , где k - коэффициент пропорциональности, y и x - пропорциональные переменные
Прямо пропорциональные величины. Две величины называются прямо пропорциональными, если с увеличением значения одной из них в несколько раз значение другой увеличивается во столько же раз.
Свойство прямой пропорциональности: x2x1=y2y1
Обратная пропорциональность.Обратная пропорциональность - это функция, заданная формулой y=xk  k
k 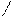 =0
=0  x
x 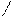 =0, где k - коэффициент пропорциональности, y и x - пропорциональные переменные
=0, где k - коэффициент пропорциональности, y и x - пропорциональные переменные
Обратно пропорциональные величины. Две величины называются обратно пропорциональными, если с увеличением значения одной из них в несколько раз значение другой уменьшается во столько же раз.
Свойство обратной пропорциональности: x2x1=y1y2
