Введя обозначения

(7.108)

и

(7.109)

преобразуем формулы (7.96) и (7.107) к следующему виду:

(7.110)

(7.111)

(7.112)

(7.113)

Поделив обе части выражения (7.89) на а_кр² представим его в виде

или

откуда

(7.114)

и

(7.115)

Связь между числами М и 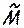приведем в таком виде:

(7.116)

Пересчет давлений и плотностей заторможенного потока из абсолютного движения в относительное и обратно удобно производить с помощью газодинамических функций, основываясь на том, что р и ρ сохраняют свои значения независимо от системы координат, а именно:

(7.117)

(7.118)

Рассмотрим связь относительной скорости w с площадью поперечного сечения потока для изоэнтропного относительного движения, когда трение и теплообмен отсутствуют.

В уравнении неразрывности ρwF=соnst, записанном в дифференциальном виде

представим dρ/ρ так:

помня, что dр/dρ=а². Величину dр/ρ найдем из уравнения Бернулли (7.94), которое для изоэнтропного течения примет вид

Тогда

Подставив это в уравнение неразрывности, получим

udu / а² – wdw / а²+ dw / w + dF / F = 0,

или

(7.119)

Из этого уравнения видно, что изменение относительной скорости в каналах рабочего колеса связано не только с формой канала, но и с его расстоянием от оси вращения. Если это расстояние постоянно, т.е. u=соnst, то уравнение (7.119) превращается в уравнение Гюгонио, следовательно, закон изменения скорости ничем не отличается от такового для неподвижных каналов. Увеличение и вдоль потока действует в ту же сторону, что и расширение канала — замедляет дозвуковой поток и разгоняет сверхзвуковой.

Если канал имеет форму сопла Лаваля, то критическое сечение может получиться в различных местах, в зависимости от закона изменения переносной скорости u. Положив в уравнении (7.119) М=1, имеем условие, определяющее местоположение критического сечения

При u=соnst dF=0, т.е. критическое сечение находится в горле. При d(u²/2)>0 dF<0, следовательно, оно располагается в суживающейся части, а при d(u²/2)<0 – в расширяющейся, так как dF>0 (рис. 166). Этим трем случаям соответствует такой характер изменения параметров торможения в относительном движении:

1. .

2. .

3. .

[1] См. файл Уравнение неразрывности.pdf

[2] В некоторых иностранных литературных источниках понятия конфузора и диффузора связывают не с изменением скорости, а с изменением площади: суживающийся канал называют конфузором, а расширяющийся — диффузором.

[3] См. файл Газодинамические функции.pdf

[4] Увеличение скорости за счет трения, кажущееся на первый взгляд парадоксальным, объясняется довольно просто. В результате преодоления сил трения уменьшается давление. В сжимаемой жидкости это приводит к падению плотности, следовательно, при постоянной площади сечения скорость должна возрастать. В несжимаемой жидкости скорость будет сохраняться постоянной.

[5] См., напр.: Л.А.Вулис. Термодинамика газовых потоков, Энергоиздат, 1950.

[6] В магнитной газодинамике работа сил электростатического или электромагнитного поля не называется внешней механической и учитывается специальными членами, входящими в уравнения.

[7] Знак минус появился в связи с тем, что, вычисляя работу, совершенную газом, надо брать момент, с которым струя действует на лопатки, тогда как уравнение (3.45) определяет момент, с которым лопатки действуют на струю.

[8] В теории косых скачков уплотнения применялась аналогичная величина — температура частичного торможения Т*.