Метод наименьших квадратов (МНК).

Помимо двух вышеописанных способов оценки погрешности результата при косвенных измерениях, иногда применяют еще так называемый «метод наименьших квадратов» или сокращенно МНК. Этот метод можно использовать, если известен вид функциональной зависимости между измеряемыми физическими величинами, а требуется определить коэффициенты, входящие в эту функцию. В наших лабораторных работах предлагается применять этот метод для определения параметровлинейной зависимости.

Пусть в эксперименте можно измерить ряд значений некоторой величины x и, соответствующие им значения, величины y. И пусть при этом известно, что между ними справедлива зависимость вида: y = ax + b. Как известно, такая зависимость графически представляется прямой линией (рис.4). Однако измеренные значения x_i и y_i включают в себя погрешность и, в результате, не лягут идеально на прямую линию.

Как по данным экспериментальных наблюдений наилучшим образом найти коэффициенты a и b? Графически эта задача сводится к построению прямой, ближе всего лежащей ко всем экспериментальным токам, так как прямая однозначно задается этими коэффициентами(рис.4.).

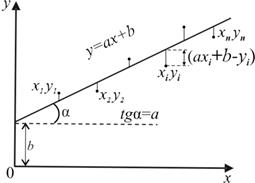	Для аналитического выражения коэффициентов применяется метод наименьших квадратов. Утверждается, что наилучшей будет та прямая, сумма квадратов расстояний до которой, от всех экспериментальных точек будет минимальной. Расстояние (вдоль оси y) от точки с координатами xi, yi до искомой прямой определяется выражением: (axi +b -yi),
Рис.4

тогда сумма квадратов расстояний будет равна:

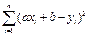
Решение задачи на нахождение минимума этого выражения (см. приложение, § 7) приводит к следующим выражениям для коэффициентов a и b.

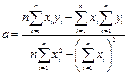	(25)
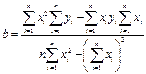	(26)

Дисперсию отклонения экспериментальных точек от прямой - S₀² и дисперсию коэффициентов a и b - S_a² и S_b² можно вычислить по формулам:

S02 =	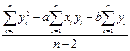(27)
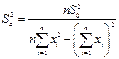	(28)
Sb2=	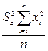(29)

Доверительные интервалы для коэффициентов a и b определяются как обычно:

Da_p = 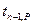S_a Db_p = 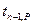S_b

Если график исследуемой зависимости проходит через начало координат, то есть b =0, формулы 25, 27 и 28 существенно упрощаются. В этом случае коэффициент a и его дисперсию можно рассчитать по следующим формулам:

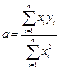	(30)
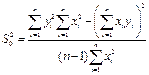	(31)
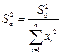	(32)

Однако следует иметь в виду, что формулы 25-28 включают разности больших величин, мало отличающихся друг от друга, что легко может привести к ошибкам при вычислениях, если их проводить с недостаточным числом значащих цифр. Поэтому все промежуточные вычисления следует выполнять с большим числом значащих цифр, без округления. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, а результаты измерений имеют более трех верных знаков, то велика вероятность получить неправильный результат вычислений. В этом случае рекомендуется для вычисления коэффициентов a и b, а также доверительных границ их погрешности вместо вышеуказанных формул использовать выражения, преобразованные к другому виду:

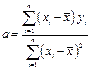	(33)
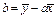	(34)
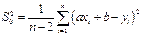	(35)
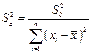	(36)
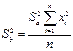	(37)

Во всех случаях проведения расчетов по МНК для определения коэффициентов линейной зависимости и их погрешностей необходимо вычислить некоторые суммы. Для этого удобно воспользоваться следующими таблицами – алгоритмами вычислений. Подсчитав суммы в каждом столбце и подставив их в соответствующие формулы, легко определить и значения a, b, Da и Db

Таблица 5

xi	yi	xi2	yi2	xi yi
x1	y1	x12	y12	x1 y1
x2	y2	x22	y22	x2 y2
…	…	…	…	…
xn	yn	xn2	yn2	xn yn
åxi	åyi	åxi2	åyi2	åx1 y1

Или в случае использования формул 33 -37

Таблица 6