Исследование устойчивости САУ по алгебраическому критерию.

Исследование устойчивости по алгебраическому критерию можно произвести либо по критерию Гурвица, либо по критерию Рауса.

Устойчивость по Гурвицу.

САР устойчива по критерию Гурвица, если при положительности коэффициентов характеристического ,уравнения все определители Гурвица, составленные по определённой схеме, положительны. Если хотя бы один из определителей Гурвица отрицательный, то система неустойчива.

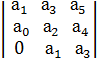
Характеристическое уравнение – это знаменатель передаточной функции приравненный к нулю.

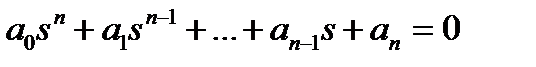
Матрица, по которой определяются все n определителей Гурвица, имеет вид

.

Итак, для устойчивости САР необходимо, чтобы:

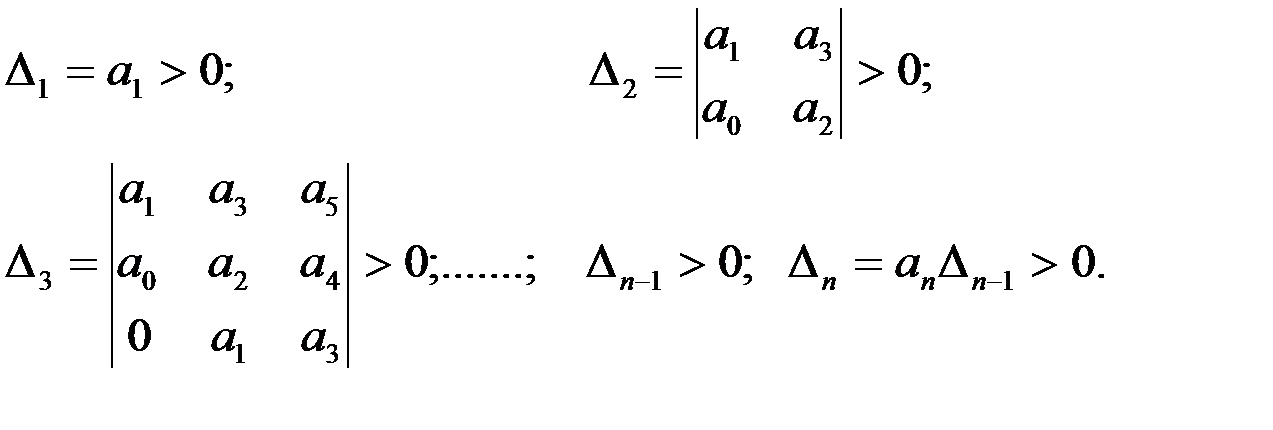
Пример:

Замкнутая передаточная функция управляющему воздействию, рассчитанная в пункте 4.1.1, имеет вид:

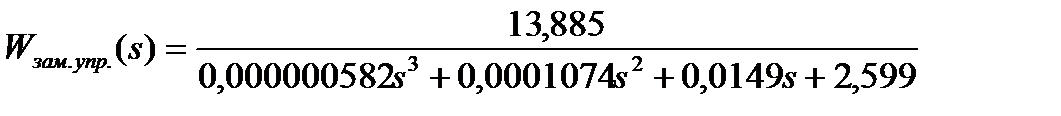
Характеристическое уравнение имеет вид:

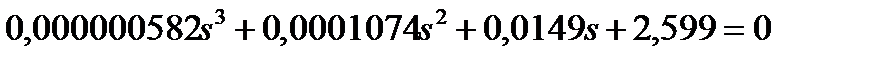
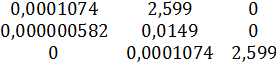
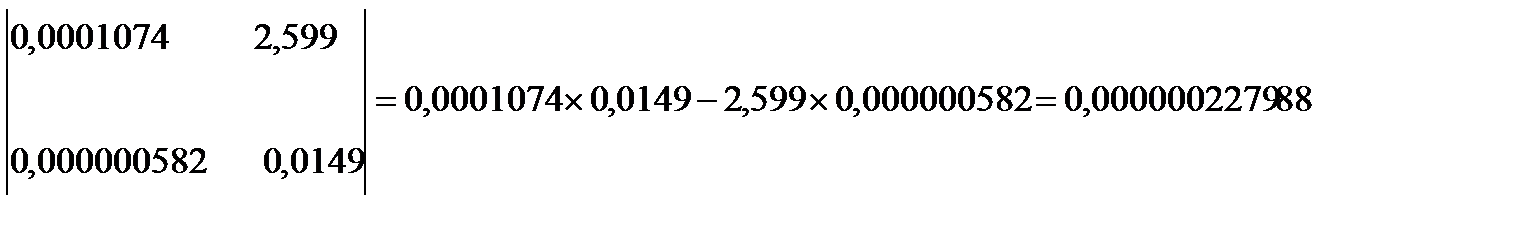
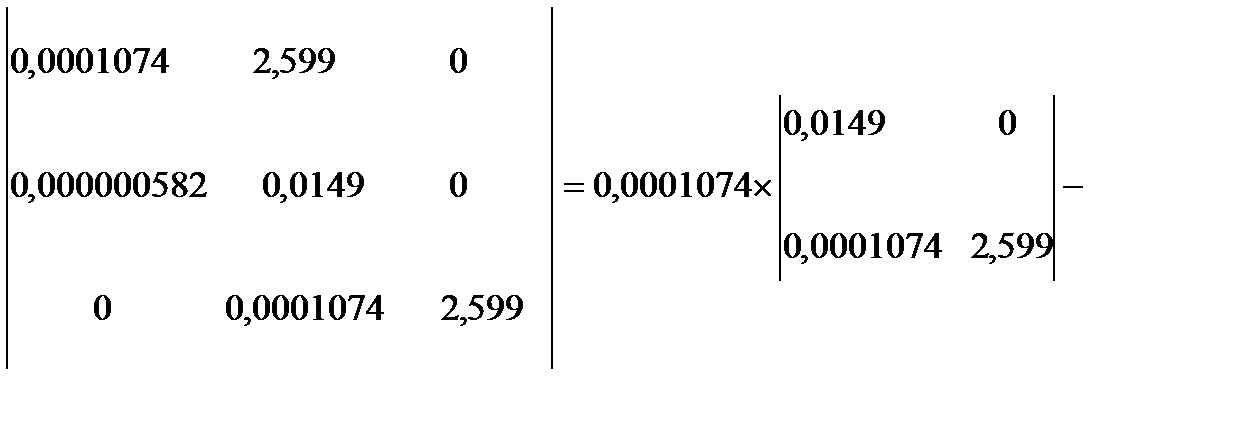
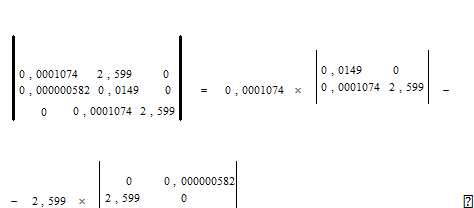
Исследование устойчивости САУ по критерию Михайлова.

Критерий Михайлова основан на рассмотрении характеристического уравнения САР, в котором вместо s используется jw. В этом случае имеем функцию комплексной переменной вида

F ( jw ) = U (w ) + j V(w ), (6)

где

U (w ) = ;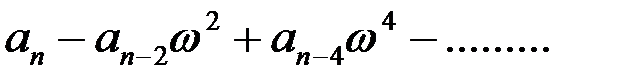

V(w ) = .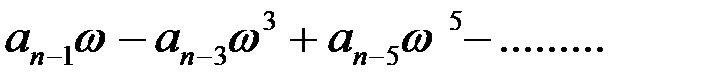

Система устойчива по критерию Михайлова, если при изменении частоты w от 0 до +¥ годограф Михайлова повернётся в положительном направлении (против часовой стрелки), начиная с вещественной положительной полуоси, на число квадрантов, равное порядку характеристического уравнения, то есть на угол np / 2, при этом нигде не обращаясь в нуль. Если годограф Михайлова проходит через начало координат, то САР находится на границе устойчивости. САР неустойчива по критерию Михайлова, если годограф проходит n квадрантов непоследовательно или проходит меньшее число квадрантов. На рис. 14,а приведены годографы Михайлова для устойчивой САР (кривая 1), для САР на границе устойчивости (кривая 2), а на рис. 14,б для неустойчивой САР при n = 4.

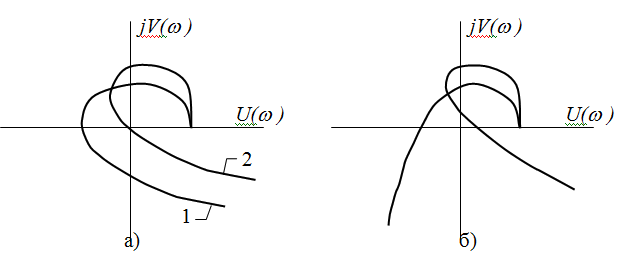
Рисунок 14. Годографы Михайлова

Пример

Система устойчива по критерию Михайлова, если годограф Михайлова повернётся в положительном направлении (против часовой стрелки), начиная с вещественной положительной полуоси, на число квадрантов, равное порядку характеристического уравнения, то есть на угол np / 2, при этом нигде не обращаясь в нуль

Замкнутая передаточная функция управляющему воздействию имеет вид:

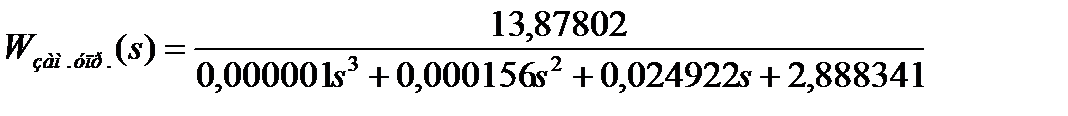
Характеристическое уравнение имеет вид:

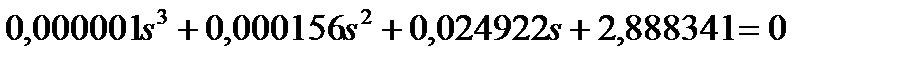
Критерий Михайлова основан на рассмотрении характеристического уравнения САР, в котором вместо s используется jw. В этом случае имеем функцию комплексной переменной вида:

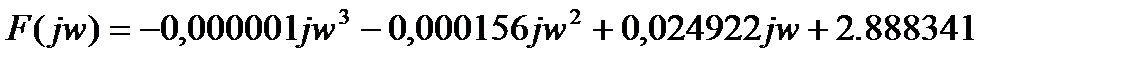
Выделим вещественную и мнимую части:

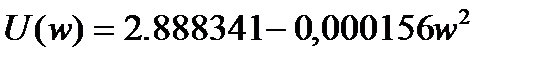
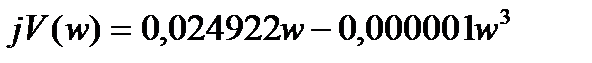
Построим график, используя MicrosoftExel.

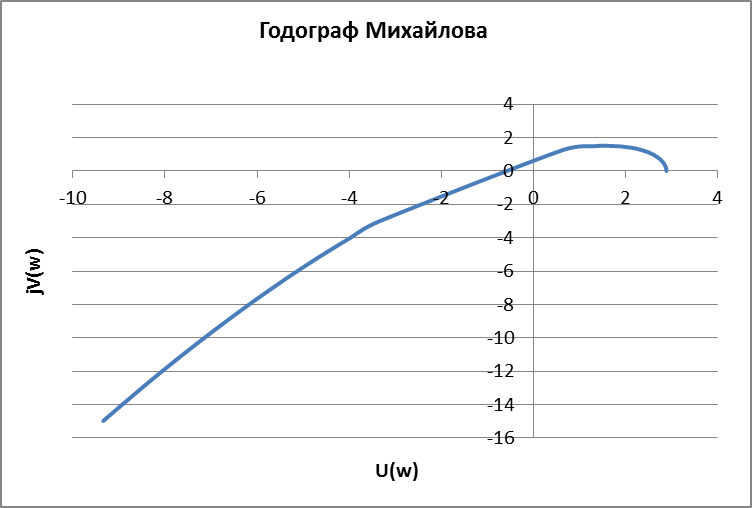
Рисунок 15 – Определение запасов устойчивости по годографу Михайлова

Таблица 2 - Годограф Михайлова
W	U(w)	jV(w)
	2,888341
0,1	2,88833944	0,002492199
0,2	2,88833476	0,004984392
0,3	2,88832696	0,007476573
0,4	2,88831604	0,009968736
0,5	2,888302	0,012460875
0,6	2,88828484	0,014952984
0,7	2,88826456	0,017445057
0,8	2,88824116	0,019937088
0,9	2,88821464	0,022429071
	2,888185	0,024921

Продолжение таблицы 2
	2,887717	0,049836
	2,886937	0,074739
	2,885845	0,099624
	2,884441	0,124485
	2,882725	0,149316
	2,880697	0,174111
	2,878357	0,198864
	2,875705	0,223569
	2,872741	0,24822
	2,825941	0,49044
	2,747941	0,72066
	2,638741	0,93288
	2,498341	1,1211
	2,326741	1,27932
	2,123941	1,40154
	1,889941	1,48176
	1,624741	1,51398
	1,328341	1,4922
	0,641941	1,26264
	-3,351659	-3,0156
	-3,991259	-4,02738
	-4,662059	-5,16516
	-5,364059	-6,43494
	-6,097259	-7,84272
	-6,861659	-9,3945
	-7,657259	-11,09628
	-8,484059	-12,95406
	-9,342059	-14,97384