Геометричні побудови на площині
Поняття конструктивної задачі на площині. Аксіоми конструктивної геометрії. Аксіоми циркуля і лінійки. Загальна схема розв’язку конструктивної задачі: аналіз, побудова, доведення та дослідження. Зміст кожного етапу розв’язку задачі та його особливості. Елементарні та найпростіші побудови на площині за допомогою циркуля та лінійки:
· поділити даний відрізок навпіл;
· побудувати перпендикуляр до даної прямої у даній точці;
· через дану точку провести пряму, паралельну даній прямій;
· поділити даний відрізок на задану кількість рівних частин;
· поділити даний відрізок у заданому відношенні;
· провести перпендикуляр з даної точки на дану пряму;
· поділити даний кут навпіл;
· побудувати кути в 30о, 45о та 60о;
· при даній вершині і даному проміні побудувати кут, рівний даному куту;
· побудувати трикутник по трьом його сторонам;
· провести коло, яке проходить через три дані точки;
· побудувати коло, вписане в даний трикутник;
· побудувати коло даного радіуса, яке проходить через дві дані точки;
· побудувати центр даного кола;
· побудувати центр даної дуги кола;
· розділити дану дугу кола на дві рівні частини;
· побудувати коло, описане навколо правильного многокутника;
· побудувати коло, вписане в правильний многокутник;
· провести з даної точки дотичну до даного кола;
· побудувати спільну дотичну до двох даних кіл;
· побудувати геометричне місце точок, які ділять навпіл хорди, що виходять з однієї точки кола;
· знайти геометричне місце точок, відстані яких до двох даних точок знаходяться у даному відношенні;
· побудувати геометричне місце точок, з яких даний відрізок видно під даним кутом.
Основні методи розв’язання конструктивних задач та їх особливості: метод перетворень, метод геометричних місць точок та алгебраїчний метод. Основна теорема конструктивної геометрії. Елементарні побудови відрізка хпо заданим відрізкам a, b, c, d,...,якщодовжина відрізка хпов’язана з довжинами заданих відрізків формулою:
1) 
;
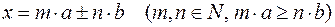2) 
;
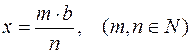3) 
;
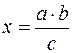4) 
;
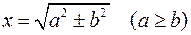5) 
,
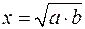та деякі більш складні побудови:
6) 
;
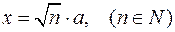7) 
;
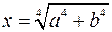8) 
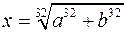
9) 
;
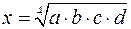10) 
;
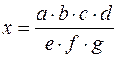11) 
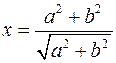та інші.
По заданим відрізкам a, b, c, d,...побудувати кутa, якщо:
1) 
;
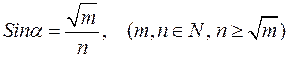2) 
;
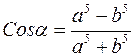3) 
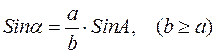, і A – деякий даний кут;
4) 
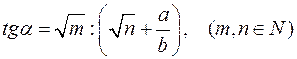та інші.
Класичні конструктивні задачі, які не розв’язуються за допомогою циркуля та лінійки: подвоєння кубу, квадратуру круга, трисекція кута та побудова правильних многокутників. Геометричні побудови на площині з застосуванням інших, крім циркуля та лінійки, інструментів.
СТЕРЕОМЕТРІЯ
ЗОБРАЖЕННЯ ГЕОМЕТРИЧНИХ ФІГУР
У ПАРАЛЕЛЬНІЙ ПРОЕКЦІЇ
Означення зображення геометричної фігури у паралельній проекції.
Властивості зображень у паралельній проекції:
· зображенням точки є точка;
· зображенням прямої є пряма;
· зберігається належність точки до прямої;
· зберігається паралельність прямих;
· зберігається відношення паралельних відрізків;
· зображенням довільного трикутника може служити довільний інший трикутник;
· зображенням кола може служити довільний еліпс;
· зображенням довільного тетраедра може служити довільний чотирикутник разом з його діагоналями (теорема Польке-Шварца).
· («антівластивість») при паралельному проектуванні лінійні розміри фігури, кути та площі фігур у загальному випадку не зберігаються.
Зображення многокутників: паралелограма, квадрата, ромба та правильного шестикутника. Зображення кола, побудова його центру та спряжених діаметрів. Побудова зображення дотичної до кола у даній точці. Побудова зображень вписаного (або описаного) правильного трикутника, квадрата, прямокутника, правильного п’ятикутника, шестикутника або восьмикутника.
Побудова зображень піраміди, призми, циліндра та конуса. Зображення сфери, паралелі та меридіани, екваторіальна площина та її полюси.
Пряма та обернена теорема Дезарга.
Метричні та позиційні задачі на проекційному кресленні.
Побудова перетинів многогранників, циліндра та конуса площиною по заданих її елементах (три точки, точка і пряма і т.п.).
ПРЯМІ ТА ПЛОЩИНИ
Кут між прямою та площиною. Кут між двома площинами. Паралельність прямої і площини. Ознака паралельності. Ознака перпендикулярності прямої та площини. Ознака паралельності площин. Необхідна та достатня умови паралельності площин. Теорема про три перпендикуляри. Теорема Фалеса у просторі.
Задачі на побудову у просторі.
Теорема Піфагора у просторі. Для прямокутного тетраедра (у якого три плоскі кути при вершині прямі), виконується співвідношення:
.
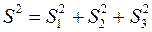Тобто, квадрат площі основи дорівнює сумі квадратів площ бічних граней.
Якщо пряма L утворює з трьома взаємно перпендикулярними прямими кути a, b, і g, то 
.
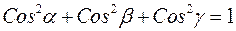МНОГОГРАННИКИ
Призма та паралелепіпед. Об’єм і площа поверхні. Діагональ прямокутного паралелепіпеда d зв’язана з його ребрами a, b, c співвідношенням: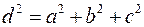 
.
Піраміда. Правильна піраміда. Об’єм і площа поверхні. Зрізана піраміда. Формула для обчислення об’єму зрізаної піраміди:
.
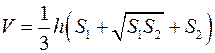В частинному випадку бічна поверхня правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ на апофему.
Об’єм правильної зрізаної чотирикутної піраміди обчислюється за формулою:
.
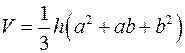Площа поверхні та об’єм правильної піраміди. Площа поверхні піраміди, у якої всі грані мають однаковий нахил до основи: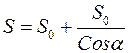 
, де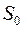 
– площа основи. Подібність многогранників.
Правільні многогранники. Теорема Ейлера для многогранників. Протилежні ребра правільного тетраедра ортогональні. У тетраедрі сума відстаней від довільної внутрішньої точки до його граней є стала величина.
КРУГЛІ ТІЛА
Конічні та циліндричні поверхні. Циліндр та конус. Об’єм і площа поверхні.
Зрізаний конус. Об’єм і площа поверхні. Сфера і куля, їх властивості. Площа сферичної поверхні та її частин. Об’єм кулі та її частин. Вписана та описана сфера, її властивості (конус, циліндр, піраміда і призма). Перша теорема Гюльдена. Друга теорема Гюльдена.
ВЕКТОРИ У ПРОСТОРІ
Додавання та віднімання векторів. Множення вектора на число. Лінійна залежність векторів. Розкладання вектора на компоненти. Проекція вектора на вісь. Координати вектора на площині та у просторі. Скалярний добуток двох векторів. Обчислення довжини вектора. Кут між двома векторами. Застосування скалярного добутку векторів до розв’язання геометричних задач.
КОРДИНАТНИЙ МЕТОД
Прямокутна декартова система координат на площині. Полярна система координат. Залежність між прямокутними та полярними координатами. Прямокутна декартова система координат у просторі. Рівняння прямої на площині. Різні способи завдання рівняння прямої на площині. (Рівняння прямої у відрізках, рівняння прямої, що проходить через дві дані точки і т.п.). Кутовий коефіціент прямої. Нормальне рівняння прямої. Відстань від точки до прямої. Коло, еліпс, гіпербола та парабола. Прямі і площини у просторі. Нормальне рівняння площини. Відстань від точки до площини. Поверхні у просторі. Рівняння сфери, тору. Еліпсоїда.
ЛІТЕРАТУРА
Адамар Ж. Элементарная геометрия. Ч.1,2. М. Учпедгиз, 1957-58.
Александров И.И. Сборник геометрических задач на построение. М. Учпедгиз, 1950.
Аргунов Б.И, Балк М.Б. Элементарная геометрия. М., Просвещение, 1966. – 366 с.
Атанасян Л.С. и др. Сборник задач по элементарной геометрии. М., Учпедгиз, 1958. – 95 с.
Барыбин К.С. Сборник геометрических задач на доказательство. М. Учпедгиз, 1962.
Бескин Л.Н. Стереометрия. М. Просвещение, 1971.
Болтянский В.Г., Яглом И.М. Векторы в курсе геометрии средней школы. М., Учпедгиз, 1962.
Выгодский М.Я. Справочнник по элементарной математике.
Киселев А.П. Геометрия. ч.1. Планиметрия. ч.2. Стереометрия. М., Просвещение, 1974.
Киселев А.П., Геометрия. Учебник и сборник задач для 9 класса. К., Радянська школа, 1963.
Кокстер Г.С. Введение в геометрию. М., Наука, 1966. – 648 с.
Кокстер Г.С., Грейтцер С.Л. Введение в геометрию. М., Наука, 1978. – 223 с.
Курант Р., Роббинс Г. Что такое математика? М., Просвещение, 1967.
Кушнир И.А. Векторные методы решения задач. К., «Обериг», 1994. – 207 с.
Кушнір І. Повернення втраченої геометрії. К., «Факт», 2000. – 279 с.
Кушнір І. Геометричні формули що не ввійшли до шкільних підручників. Довідник. К., «Факт», 2002. – 111 с.
Кымпан Ф. Истрия числа p. М., Наука, 1971. – 216 с.
Литцман В. Теорема Пифагора. М., Физматгиз, 1960. – 114 с.
Лоповок Л.М. Сборник геометрических задач для 10 класса. К., «Радянська школа», 11979. – 95 с.
Лоповок Л.М. Збірник задач з геометрії для 9-10 класів. К., «Радянська школа», 1984. – 120 с.
Лоповок Л.М. Факультативные задания по геометрии для 7-11 классов. К., «Радянська школа», 1990. – 128 с.
Моденов П.С. Сборник задач по специальному курсу элементарной математики. М., Советская наука, 1957. – 666 с.
Назаретский В.Е., Федин Н.Г. Задачник-практикум по элементарной геометрии. М., Просвещение, 1965. – 163 с.
Никулин А.В., Кукуш Н.Г., Татаренко Ю.С. Планиметрия. Геометрия на плоскости. Висагинас, «Альфа», 1998. – 588 с.
Никулин А.В., Кукуш Н.Г., Татаренко Ю.С. Стереометрия. Геометрия в пространстве. Висагинас, «Альфа», 1998. – 574 с.
Перепелкин Д.И. Курс элементарной геометрии. Ч. 1,2.
Прасолов В.В. Задачи по планиметрии. Ч.1. М., Наука, 1986. – 270 с.
Прасолов В.В. Задачи по планиметрии. Ч.2. М., Наука, 1991. – 239 с.
Прасолов В.В. Задачи по стереометрии. М., Наука, 1989. – 286 с.
Пойа Д. Как решать задачу. М., Учпедгиз РСФСР, 1959. – 207 с.
Пойа Д. Математическое открытие. М., Наука, 1970. – 452 с.
Пойа Д. Математика и правдоподобные рассуждения. М., Наука, 1975. – 462 с.
Ривкин А.А. и др., Справочник по элементарной математике. М., Высшая школа, 1964.
Савченко В.М. Изображение фигур в математике. К., «Вища школа», 1978. – 133 с.
Справочник по элементарной математике. Геометрия. (Под редакцией Фильчикова). К., Наукова думка, 1966.
Скопец З.А., Жаров В.А. Задачи и теоремы по геометрии. Планиметрия. М., Учпедгиз, 1962. – 164 с.
Тесленко І.Ф. і ін. Практикум з розв’язування задач. К., «Вища школа», 1978. – 206 с.
Филипповский Г. Школьная геометрия в миниатюрах. К., «Грот», 2002. – 238 с.
Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. М., Просвещение, 1989. – 192 с.
Цыпкин А.Г., Справочник по математике. Наука, М., 1988.
Шарыгин И.Ф. Геометрия. Планиметрия. 9-11 классы. От учебной задачи к творческой. М., «Дрофа», 2001. – 397 с.
Шклярский Д.О. и др. Избранные задачи и теоремы элементарной математики. Геометрия (Планиметрия. Стереометрия).
Энциклопедия элементарной математики, кн.4, М., Физматгиз, 1963.
Энциклопедия элементарной математики, кн.5, М., Наука, 1966.