Числовые характеристики дискретных СВ

II РАЗДЕЛ

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ (СВ)

Случайной называется величина, которая в процессе опыта принимает единственное значение, причем до опыта неизвестно какое именно. Будем обозначать их заглавными латинскими буквами с конца алфавита X, Y, Z , а значения СВ –строчными буквами x, y, z.

Дискретные СВ

Закон распределения дискретных СВ

Под дискретной СВ будем понимать такую СВ, которая может принимать значения изолированные друг от друга. Число возможных значений может быть как конечным, так и бесконечным.

Законом распределения дискретной СВ называют соотношение между возможными значениями СВ и их вероятностями.

Существуют три способа задания закона:

· табличный – в виде ряда распределения

			…		…
			…		…

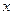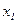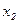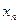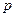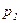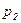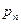· графический

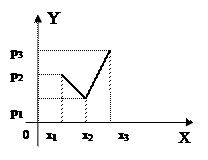
· аналитический– см. ниже функцию распределения вероятностей .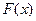

Пример 2.1.Пусть событие С появится с вероятностью р. Составить закон распределения для СВ Х – число появления С в одном испытании.

Решение:

СВ Х может принимать значение 0 (событие появилось) с вероятностью р или 1 (не появилось) с вероятностью 1-р.

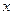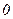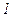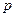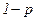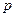Пример 2.2. Вероятность попадания в мишень первого стрелка равна 0,9, второго – 0,8. Составить закон распределения для СВ Х- числа пробоин в мишени, если каждый стрелок стреляет по одному разу.

Решение:

Пусть событие А_i – попадание в мишень i–ого стрелка, ,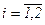

событие B_i –число пробоин.

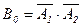. Так как события независимые, то ;

,

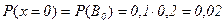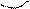
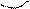
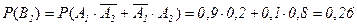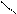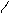несовместные

.

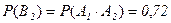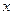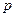	0,02	0,26	0,72

Геометрическое распределение

Пусть С может появится в одном испытании с вероятность Р, испытания проводятся до тех пор пока С не наступит в соответствии с рядом распределения Х- числа испытаний.

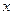				…	n	…
				…		…

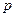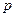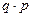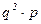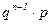Проверим равенство .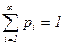

.

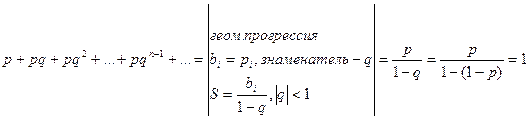Гипергеометрическое распределение

Пусть имеется 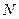деталей, из них 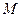-стандартных, из этой партии выбирается 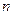деталей на проверку, причем после проверки детали не возвращаются. Пусть 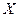– число стандартных деталей среди 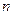отобранных. Составим ряд распределения для .

.

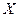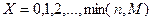Получим формулу для нахождения вероятности того, что будет выбрано m стандартных деталей.

Общее число исходов равно числу сочетаний 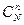, число благоприятных исходов - 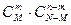(число вариантов выбора стандартных деталей и число вариантов выбора оставшихся нестандартных деталей, соответственно).

.

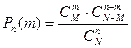Простейший поток событий

Под потоком событий будем понимать их последовательность, которая появляется в случайные моменты времени.

Простейшим называется поток событий, который обладает следующими свойствами:

· стационарностью – вероятность наступления события 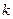раз за время 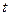, зависит только от этих чисел. 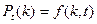. Вероятность не зависит от того, в какой момент начался отсчет;

· отсутствием последействия (для любых непересекающихся промежутков времени число появлений события на любом из них не зависит от того, сколько событий появилось на предыдущем промежутке);

· ординарностью (за малое время 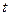вероятность появления двух и более событий пренебрежительно мала).

Под интенсивностью потока 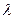будем понимать число событий, произошедших за единицу времени.

Тогда вероятность появления 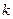событий за время 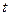будет определяться по формуле

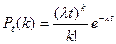
Пример2.3. Пусть в справочную службу за одну минуту поступает два звонка. Найти вероятность того, что за 5 минут

А) поступит 2 звонка,

Б) не менее двух звонков.

Решение:

.

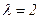А)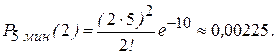

Б)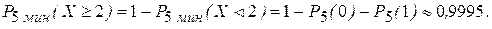

Функция распределения вероятностей (интегральная)

Функцией распределения вероятностей называется вероятность того, сто СВ примет значение меньшее значения аргумента функции .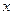

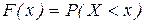
Пример 2.4. Составить 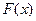для СВ X (оценка на экзамене по пятибальной шкале), заданной рядом распределения

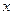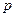	0,1	0,3	0,4	0,2

Решение:

Пусть 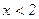, 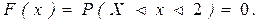Если , .

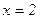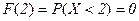Пусть 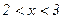, 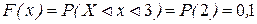. Если ,

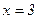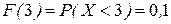
Пусть 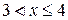, 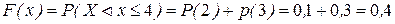. и так далее.

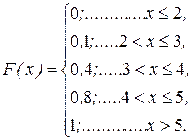
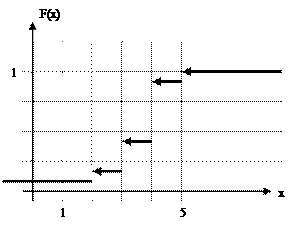
Для любой дискретной СВ график 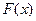представляет “лесенку”.

Свойства :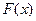

1. предельное .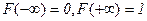

2. область изменения функции .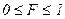

3. 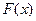-неубывающая функция,

,

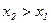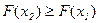
Доказательство:

,

,

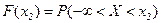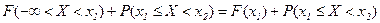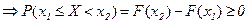, т.е. .

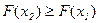4.

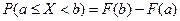
Числовые характеристики дискретных СВ

Закон распределения полностью описывает рассматриваемую СВ. Однако для многих задач практики достаточно знать только несколько чисел, характеризующих данную СВ.

К ним относятся такие числовые характеристики как математическое ожидание 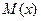, дисперсия 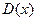, среднее квадратическое отклонение 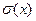, мода, медиана, начальные и центральные моменты распределения.

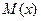характеризует среднее значение СВ, 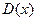и 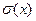- разброс СВ относительно среднего.

Математическое ожидание

Математическим ожиданием дискретной СВ называется сумма произведений всех возможных значений СВ на их вероятности:

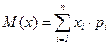
Если 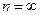, получим ряд 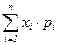, который может сходиться или расходится. В последнем случае говорят, что СВ не имеет математического ожидания.

Вероятностный смысл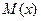

Пусть производиться 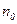опытов, в которых значение СВ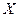

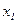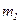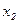появилось раз, появилось 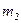раз, ..., 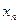появилось 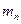раз, .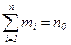

Вычислим среднеарифметическое :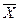

,

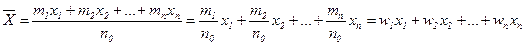где 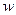- относительная частота.

При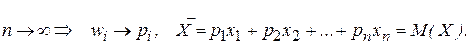

Таким образом, 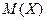- есть среднее арифметическое СВ X.

Пример 2.5.При подгонке деталей может потребоваться от одной до пяти проб. Вероятности этих событий даны в таблице(Х- число проб).

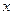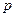	0,07	0,16	0,55	0,21	0,01

Найти среднее значение числа проб для правильной оценки производительности сборщика.

Решение:

.

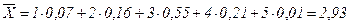Пример 2.6.Найти 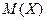числа появлений события в одном испытании

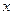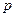	1-р	р

Решение:

.
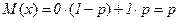