Свойства неопределенного интеграла
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное
учреждение высшего профессионального образования
Московский технический университет связи и информатики
____________________________________________________________
О.М. Смелянский
МАТЕМАТИКА
Второй семестр
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
для бакалавров по специальностям:
080100, 080200, 230700, 010300
Москва 2012
УДК 51(075.8)
Смелянский О.М. Математика, второй семестр. Учебно – методический комплекс для бакалавров: Учебное пособие / МТУСИ. - М., 2012. – 65с.
Учебно – методический комплекс представляет собой учебное пособие по математике для студентов 2 семестра экономических и технических высших учебных заведений, обучающихся по программам бакалавров по специальностям: 080100, 080200, 230700, 010300 в соответствии с государственными образовательными стандартами высшего профессионального образования третьего поколения.
Ил. 1, список лит. 11назв.
Издание утверждено Методическим советом ОТФ-1 в качестве учебного пособия. Протокол № 3 от 15.11.2012г.
Рецензенты: И.А. Гудкова, ст. преподаватель (МТУСИ)
Р.В. Арутюнян, профессор (МТУСИ)
СОДЕРЖАНИЕ
Введение. ……………………………………………………………………………………… 5 1. ИНТЕГРИРОВАНИЕ …………………………………………………………………….. 6 1.1. Неопределенный интеграл ……………………………………………………………… 6 Определения. …………………………………………………………………………………… 6 Свойства неопределенного интеграла. Таблица простейших неопределенных интегралов. Разложение подынтегральной функции на слагаемые. Введение функции под знак дифференциала ………………………………………………………………………………… 7 Метод подстановки. Интегрирование по частям. …………………………………………… 8 Задания для самостоятельного решения. ……………………………………………………. 9 Интегрирование рациональных выражений. ……………………………………………….. 10 Интегрирование простейших иррациональностей. ………………………………………… 12
Интегрирование тригонометрических функций …………………………………………… 13 Задания для самостоятельного решения …………………………………………………….. 14 1.2. Определенный интеграл …………………………………………………………………. 15 Геометрический смысл определенного интеграла. Свойства определенного интеграла… 15 Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница. ……………… 16 Замена переменной в определенном интеграле. ………………………………………………. 16
Интегрирование по частям в определенном интеграле. ……………………………................. 17
Вычисление площади плоских фигур …………………………………………………………. 17
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл). …….. 17
Задания для самостоятельного решения. ……………………………………………………….. 18 Контрольная работа № 1. Интегрирование. ……………………………………………………. 19 2. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ………………………………………….. 23 2.1. Основные определения. ……………………………………………………………………. 23 2.2. Частные производные функции двух переменных. Полный дифференциал. …………… 25 2.3. Производная по направлению. Градиент. ………………………………………………….. 25 2.4. Экстремум функции двух переменных. …………………………………………………… 26 Задания для самостоятельного решения. ……………………………………………………….. 27 Контрольная работа № 2. Функции нескольких переменных. ………………………………… 29 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ …………………………………………………. 32 3.1. Общие понятия ………………………………………………………………………………. 32 3.2. Дифференциальные уравнения первого порядка ……………………………………………32 Дифференциальные уравнения с разделяющимися переменными. …………………………… 33 Задания для самостоятельного решения. ……………………………………………………… 35 Однородные дифференциальные уравнения. …………………………………………………. 36 Задания для самостоятельного решения. ………………………………………………………. 36 Линейные уравнения первого порядка. Уравнение Бернулли. ………………………………. 37 Задания для самостоятельного решения. ……………………………………………………… 38 Уравнения в полных дифференциалах. ………………………………………………………… 39 Задания для самостоятельного решения. ……………………………………………………… 40 3.3. Дифференциальные уравнения высших порядков, допускающие понижение порядка. .. 40 Задания для самостоятельного решения. ………………………………………………………. 41 3.4. Линейные дифференциальные уравнения. ……………………………………………….. 42 Линейные однородные уравнения с постоянными коэффициентами. ………………………. 42 Задания для самостоятельного решения. ……………………………………………………. 43
Линейные неоднородные уравнения с постоянными коэффициентами и специальной правой частью. ………………………………………………………………………………….. 44 Задания для самостоятельного решения. …………………………………………………….. 46 Контрольная работа № 3. Дифференциальные уравнения. …………………………………. 47 4. РЯДЫ………………………………………………………………………………………… 51 4.1.Числовые ряды. …………………………………………………………………………….. 51 Основные понятия и свойства. ………………………………………………………………… 51 Необходимый признак сходимости и достаточный признак расходимости ряда. ………… 53 Достаточные признаки сходимости знакоположительных рядов. ………………………….. 53 Знакопеременные ряды ………………………………………………………………………… 55 Задания для самостоятельного решения. ……………………………………………………… 56 4.2. Функциональные ряды. ……………………………………………………………………. 57 Степенные ряды. ………………………………………………………………………………… 57 Разложение функции в степенной ряд. ………………………………………………………… 58 Ряд Маклорена. ………………………………………………………………………………….. 59 Задания для самостоятельного решения. ……………………………………………………… 61 Контрольная работа № 4 Ряды. ………………………………………………………………… 62 Вопросы к экзамену по курсу “Математика, второй семестр”. ……………………………… 64 Литература. ……………………………………………………………………………………… 65
Введение
Настоящий УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС (УМК) является руководством для освоения следующих четырех разделов математики изучаемых во втором семестре 1-го курса на факультете экономики и управления МТУСИ: 1. Интегрирование, 2. Функции нескольких переменных, 3. Дифференциальные уравнения, 4. Ряды. Уменьшение общей суммы часов аудиторных занятий, выделяемых для бакалавров, требует от студентов большей самостоятельности, и предлагаемое пособие решает возникающую при этом задачу – предоставить в краткой и ясной форме, в едином комплексе, все, что требуется для такой самостоятельной работы.
Каждый из четырех разделов снабжен кратким изложением теории и методов решения задач, иллюстрируемых примерами с подробным их решением. Кроме того, для каждой отдельной темы даны задания для самостоятельной работы. Часть рекомендуемых здесь задач может быть разобрана студентами вместе с преподавателем во время аудиторных занятий, остальные предлагаются в качестве домашней работы. В конце каждого из четырех разделов приведены 30 вариантов заданий домашней контрольной работы. В завершение дается перечень вопросов к экзамену, сдаваемому по окончании 1-го курса, и список литературы, с помощью которой каждый студент может расширить и углубить свои знания по изучаемым разделам курса. Первые два пособия в этом списке рекомендуются как основные, остальные – как дополнительные.
Таким образом, предлагаемый УМК полностью обеспечивает студентов всем необходимым материалом для аудиторной (лекции и практические занятия) и самостоятельной работы, а также для сдачи текущей отчетности (4 контрольные работы), а, затем, и экзамена по курсу “Математика” во втором семестре первого курса.
1. Интегрирование
1.1. Неопределенный интеграл
Основной операцией дифференциального исчисления является дифференцирование - нахождение производной данной функции. Обратной к этой операции является интегрирование – отыскание функции по известной ее производной. В этом разделе рассматриваются некоторые из основных методов и приемов интегрирования.
Функция 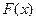 , для которой выполняется равенство
, для которой выполняется равенство 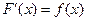 для всех
для всех  из области определения
из области определения 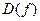 , называется первообразной функции
, называется первообразной функции 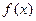 . Несколько примеров первообразных для различных функций приведем в следующей таблице.
. Несколько примеров первообразных для различных функций приведем в следующей таблице.
Таблица 1.
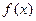 | 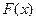 | 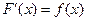 |
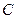 | 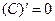 | |
 | 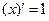 | |
 | 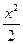 | 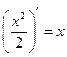 |
 | 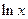 | 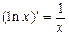 |
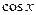 |  | 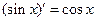 |
Если 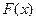 - первообразная функции
- первообразная функции 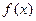 , то функция
, то функция 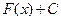 , где С – любое действительное число, также является первообразной функции
, где С – любое действительное число, также является первообразной функции 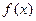 , т.к.
, т.к. 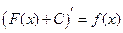 .
.
Теорема 1. Любые две первообразные 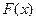 и
и 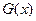 данной функции
данной функции 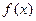 отличаются только на некоторую постоянную, т.е. существует число
отличаются только на некоторую постоянную, т.е. существует число 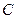 такое, что
такое, что 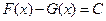 .
.
Доказательство. Поскольку 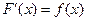 и
и 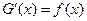 , то
, то 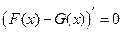 . А это означает, что
. А это означает, что 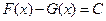 . Итак,
. Итак, 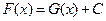 .
.
Следствие. Если 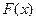 - одна из первообразных функции
- одна из первообразных функции 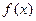 , то множество всех ее первообразных имеет вид
, то множество всех ее первообразных имеет вид 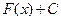 .
.
Теорема 2. Если функция непрерывна в области своего определения, то она имеет первообразную, определенную в этой же области.
Множество всех первообразных данной функции 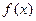 называется ее неопределенным интегралом(обозначается
называется ее неопределенным интегралом(обозначается 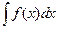 ):
): 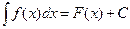 . Здесь
. Здесь  - переменная интегрирования,
- переменная интегрирования, 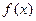 - подынтегральная функция,
- подынтегральная функция, 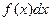 - подынтегральное выражение,
- подынтегральное выражение, 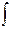 -знак неопределенного интеграла,
-знак неопределенного интеграла, 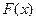 - одна из первообразных функции , С – произвольная постоянная (
- одна из первообразных функции , С – произвольная постоянная ( 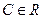 ) называемая постоянной интегрирования.
) называемая постоянной интегрирования.
Например, 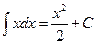 . Множество всех первообразных подынтегральной функции
. Множество всех первообразных подынтегральной функции 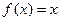 представляет собой множество парабол отличающихся от первообразной
представляет собой множество парабол отличающихся от первообразной 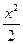 параллельным переносом по оси
параллельным переносом по оси 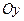 . Таким образом, все эти параболы покрывают сплошь плоскость
. Таким образом, все эти параболы покрывают сплошь плоскость 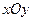 . При этом через каждую точку плоскости проходит только одна из парабол этого семейства первообразных.
. При этом через каждую точку плоскости проходит только одна из парабол этого семейства первообразных.
Свойства неопределенного интеграла.
I.  . II.
. II. 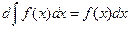 , или
, или  .
.
III. 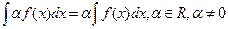 . IV.
. IV. 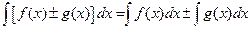 .
.
Таблица простейших неопределенных интегралов.
1. 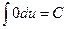 ,
,  . 7.
. 7. 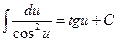 .
.
2. 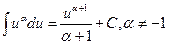 . 8.
. 8. 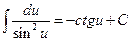 .
.
3. 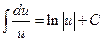 . 9.
. 9. 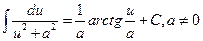 ,
, 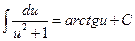 .
.
4. 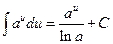 ,
, 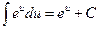 . 10.
. 10. 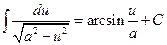 ,
, 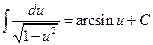 .
.
5. 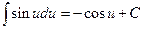 . 11.
. 11. 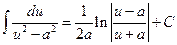 .
.
6. 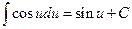 . 12.
. 12. 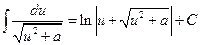 .
.
