Побудова області стійкості по двох параметрах
Розглянемо випадок впливу двох параметрів на стійкість системи. При цьому решта всіх параметрів системи повинна бути задані. В якості варійованих параметрів, як правило, приймають постійну часу Т одного з конструктивних елементів системи і передавальний коефіцієнт k розімкненого контуру або одного з елементів. Варійовані параметри k і Т повинні входити в характеристичне рівняння системи лінійно, тобто рівняння не містить перемножень k і Т і їх ступенів вище першою. Характеристичне рівняння може бути представлене в наступному вигляді:
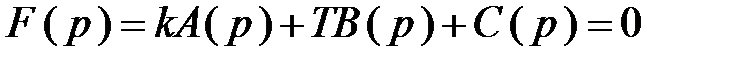 , (1)
, (1)
де A(p), B(p), C(p) - поліноми від р, коефіцієнти яких не залежать від k і Т.
Якщо варійовані параметри входять в рівняння нелінійно, то слід ввести такі дві нові змінні, які були б функціонально пов'язані з k і Т і входили б в рівняння лінійно.
Згідно загальній методиці D-розбиття підставимо в характеристичне рівняння (1) замість змінній р уявний корінь jω. Тоді отримаємо тотожність
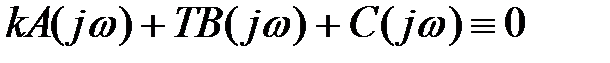 , (2)
, (2)
яке при кожному фіксованому значенні ω можна розглядати як рівняння з невідомими k і Т.
Кожен з трьох поліномів, що входять в рівняння (2), після зведення jω в парні і непарні ступені можна представити у вигляді суми дійсної і уявної частин:
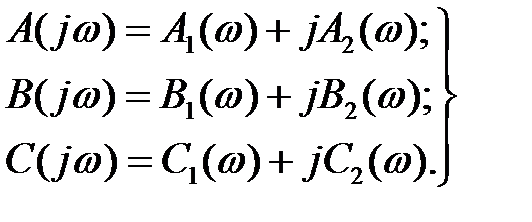 (3)
(3)
Підставляючи (3) в (2) і групуючи дійсні і уявні доданки, отримаємо
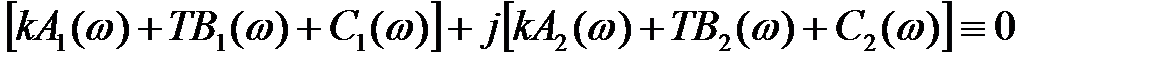 (4)
(4)
Відомо, що комплексна величина дорівнює нулю тоді, коли одночасно дорівнюють нулю її дійсна і уявна частини. Тому, умова (4) еквівалентна двом рівнянням:
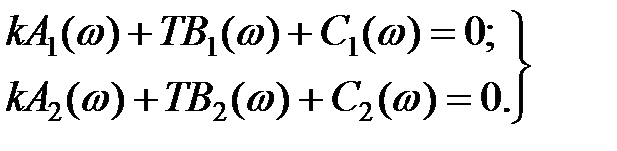 (5)
(5)
Ця система двох рівнянь дає можливість визначити для кожного фіксованого значення ω два невідомих k і Т.
Для вирішення системи (5) скористаємося методом визначників:
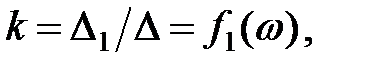 (6)
(6)
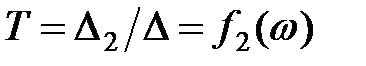 (7)
(7)
де
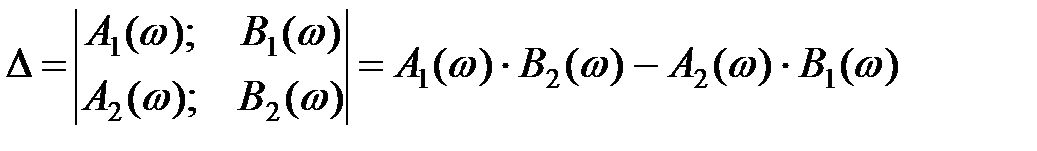 ; (8)
; (8)
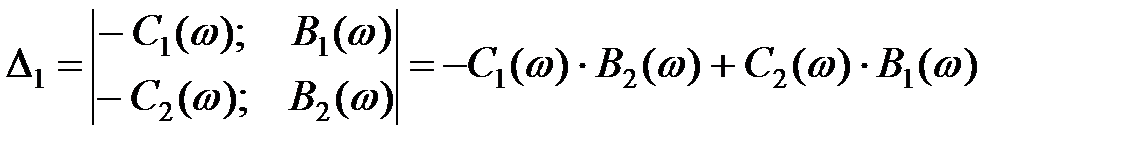 ; (9)
; (9)
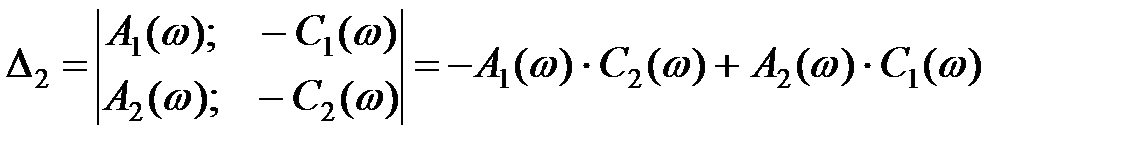 . (10)
. (10)
Вирази (6) і (7) є рівнянням кривої D-розбиття, заданим в параметричній формі. Підставляючи в ці вирази різні значення параметра ω (у діапазоні від -  до +
до +  ), можна побудувати основну межу області стійкості (рис. крива АВС).
), можна побудувати основну межу області стійкості (рис. крива АВС).
Оскільки поліноми А1(ω), В1(ω), С1(ω) - парні функції, а поліноми А2(ω), В2(ω), С2(ω) - непарні, то визначники Δ, Δ1 і Δ2 є непарними функціями змінної ω; відповідно f1(ω) і f2(ω) - парні функції ω. З цього виходить, що крива D-розбиття при зміні ω від - 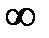 до +
до + 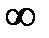 проходить двічі через одні і ті ж точки: перший раз при зміні ω від -
проходить двічі через одні і ті ж точки: перший раз при зміні ω від - 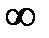 до 0 і другий раз - при зміні ω від 0 до +
до 0 і другий раз - при зміні ω від 0 до + 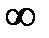 .
.

Рисунок Область стійкості в площині двох параметрів.
Крива D-розбиття, побудована в площині двох параметрів, штрихується за наступним правилом:
якщо головний визначник Δ > 0, то штрихування наноситься зліва (при русі уподовж кривої у бік збільшення ω); якщо визначник Δ< 0, то штрихування наноситься справа. Це правило сформульоване стосовно цілком певного порядку побудови кривої D-розбиття: рівняння, що виходить від прирівнювання до нуля дійсної частини, повинне бути записане в першому рядку системи (5); параметр, що стоїть на першому місці, необхідно відкладати по осі абсцис.
Оскільки при проходженні змінної ω через нуль знак головного визначника Δ міняється на протилежний, то штрихування кривої D-розбиття завжди подвійне.
Рівняння (5) визначають в площині k - T одну єдину крапку (при фіксованому значенні ω) лише у тих випадках, коли ці рівняння сумісні і лінійно незалежні, тобто коли визначники Δ, Δ1 і Δ2 не дорівнюють нулю. Якщо ж при деякому значенні ω всі три визначники одночасно звертаються в нуль або нескінченність, то рішення (6) і (7) стають невизначеними. Це означає, що при даному значенні ω рівняння (5) еквівалентні, тобто одне відрізняється від іншого на постійний множник. У системі координат k - Т таким «винятковим» значенням ωИ відповідають так звані особливі прямі (див. рис., прямі ВF, АЕ і СЕ). Рівнянням персоною прямої може служити будь-яке з рівнянь (5):
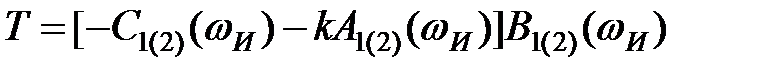 , (11)
, (11)
де ωИ - "виняткові" частоти, при яких всі три визначники Δ, Δ1 і Δ2 одночасно звертаються в нуль або в нескінченність і рішення (6) і (7) стають невизначеними.
У багатьох практичних завданнях параметри k і Т входять в старший коефіцієнт a0 або вільний коефіцієнт an характеристичного рівняння системи. В цьому випадку рівняння двох особливих прямих отримують прирівнюванням вказаних коефіцієнтів до нуля:
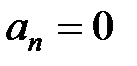 ;
; 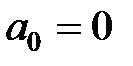 . (12)
. (12)
Перше рівняння відповідає ωИ = 0, а друге - ωИ = 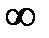 .
.
Штрихування особливих прямих виконують по наступних правилах. Особливі прямі, відповідні ωИ = 0 і ωИ = 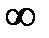 , штрихують один раз (прямі АЕ і СЕ), а прямі, відповідні 0 < ω <
, штрихують один раз (прямі АЕ і СЕ), а прямі, відповідні 0 < ω < 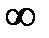 , штрихують двічі (прямі ВF). В точках перетину (або сполучення) персоною прямої з кривій D-розбиття, відповідних ω = ωИ, заштриховані сторони прямої і кривої повинні бути звернені один до одного (точки А,В,С). Причому, якщо в точці перетину визначник Δ міняє знак, то штрихування персоною прямої переходить на протилежну сторону прямої, якщо ж знак визначника не міняється, то напрям штрихування залишається тим самим.
, штрихують двічі (прямі ВF). В точках перетину (або сполучення) персоною прямої з кривій D-розбиття, відповідних ω = ωИ, заштриховані сторони прямої і кривої повинні бути звернені один до одного (точки А,В,С). Причому, якщо в точці перетину визначник Δ міняє знак, то штрихування персоною прямої переходить на протилежну сторону прямої, якщо ж знак визначника не міняється, то напрям штрихування залишається тим самим.
Після нанесення штрихування виявляють області з найбільшим числом лівого коріння.
