Геометрический и физический смысл производной

Пусть функция y=f(x) имеет производную в точке x₀. Тогда существует касательная к графику этой функции в точке М₀(x₀, у₀), уравнение которой имеет вид

.

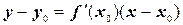При этом 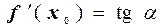, где a – угол наклона этой касательной к положительному направлению оси ОХ (рис. 2.1).

Геометрически, чтобы провести касательную, надо к графику кривой приставить линейку так, чтобы она коснулась графика в выбранной точке.

Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x₀ равен значению производной функции в этой точке.

Физический смысл: скорость тела равна первой производной координаты по времени:

V(t)=x ^/ (t). (2.1)

Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:

a(t)= V ^/ (t)=x ^// (t). (2.2)

Таблица производных

1. С ¢ = 0, где С–постоянная

2. (x^m)¢ = mx^m–1

3.

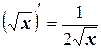
4.

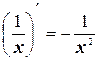
5.

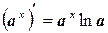
6.

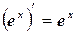
7.

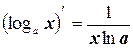
8.

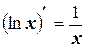
9.

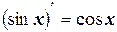
10.

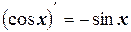
11.

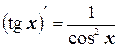
12.

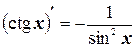
13.

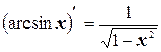
14.

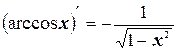
15.

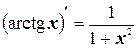
16.

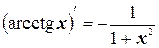
Основные правила дифференцирования

Пусть uиv – функции, дифференцируемые в точке х. Тогда

1. Производная суммы двух дифференцируемых функций равна сумме их производных:

(u+v) ′=u′+v′

2. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу:(uv) ′=u′v+uv′, в частности (Cu) ′=Cu′, С=const (постоянный множитель можно выносить за знак производной)

3. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:

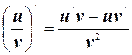, где v ¹ 0

4. Производная сложной функции равна производной по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной:y′_x=y′_{u ·} u′_x, где и – промежуточный аргумент.

Производные высших порядков

Производная f ′ (x) от функции f(x) называется также производной первого порядка. В свою очередь производная от функции f ′ (x) тоже является функцией от x , поэтому также может быть дифференцируема и называется производной второго порядка от функции f(x) (или просто второй производной).

Вторая производная обозначается символами: f′′(х) (читается: «эф два штриха от икс») или 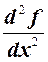(«дэ два эф по дэ икс дважды»).

Исходя из определения второй производной, можно записать: .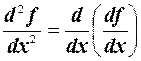

Аналогично определяется третья производная:

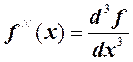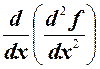= и т.д.

Производная п-ного порядка обозначается .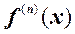

Дифференциал функции

Если функция f(х) дифференцируема в точке х₀, то ее приращение можно представить в виде

Δf(х₀) = f ^/(x₀)×Δх + α(Δх)× Δх. (2.3)

В этом случае выражение f ^/(x₀)×Δх, линейно зависящее от Δх, называется дифференциалом функции f(х) в точке х₀ и обозначается символом df(x):

df(x) = f '(x₀)·Δx.

Дифференциал функции равен произведению производной функции на приращение ее аргумента.

Термин «дифференциал» происходит от латинского слова differentia, означающего различие.

Дифференциал функции есть главная часть приращения функции. В этом состоит аналитический смысл дифференциала.

Дифференциал аргумента dx равен его приращению ∆x: dx=∆x. Поэтому можно записать df=f ^/(x)dx (дифференциал функции равен произведению производной этой функции на дифференциал аргумента).

Если приращение аргумента ∆xблизко к нулю (достаточно мало), то приращение функции Δfприближенно равно ее дифференциалу, т.е. Δf»df, откуда f(х₀+∆x) ≈ f ^/(x₀)+dfили

f(х₀+∆x) ≈ f ^/(x₀)+f ^/(x₀) ∆x(2.4)

Формула (2) используется для приближенного вычисления значения функции f(x) в точке x₀+∆x по известному значению этой функции и ее производной в точке x₀.