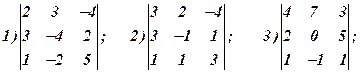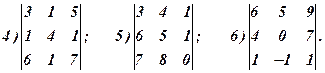Мінори. Алгебраїчні доповнення. Теорема про розклад
Означення 1. Мінором елемента 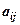 (позначається
(позначається 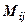 ) визначника
) визначника 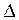 3-го порядку називається визначник 2-го порядку, отриманий з даного визначника
3-го порядку називається визначник 2-го порядку, отриманий з даного визначника 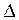 , в якому викреслено і-тий рядок і j-ий стовпець, в яких містився елемент
, в якому викреслено і-тий рядок і j-ий стовпець, в яких містився елемент 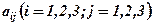 .
.
 Наприклад, викреслюючи у визначнику
Наприклад, викреслюючи у визначнику

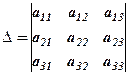
3-ій рядок 2-ий стовпець знаходимо мінор
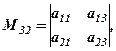
який відповідає елементу 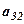 .
.
Аналогічно можна виписати мінори для решти елементів. Всього для елементів визначника 3-го порядку можна виписати 9 мінорів.
Означення 2. Алгебраїчним доповненням елемента 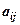 (позначається
(позначається 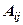 ) називається відповідний мінор
) називається відповідний мінор 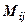 , взятий із знаком
, взятий із знаком 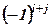 , тобто
, тобто
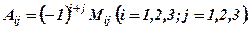
Знаки перед мінорами залежать від місця елемента 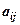 у визначнику і розподіляються за схемою:
у визначнику і розподіляються за схемою:
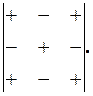
Приклад 1. Знайти алгебраїчні доповнення елементів визначника.
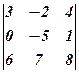 .
.
Розв’язання. Відповідно до означення алгебраїчних доповнень, ураховуючи схему розподілу знаків для відповідних мінорів, маємо
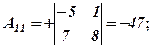
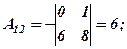
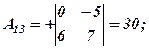
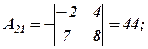
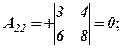
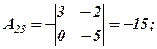
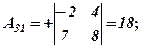
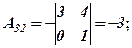
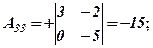
Поняття алгебраїчного доповнення дає можливість ще одного способу обчислення визначника, який стверджується наступною теоремою.
Теорема. (Про розклад визначника). Визначник дорівнює сумі добутків елементів рядка (стовпця) на їх алгебраїчні доповнення.
Наприклад,
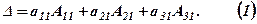
Рівність (1) перевіряється безпосередньо
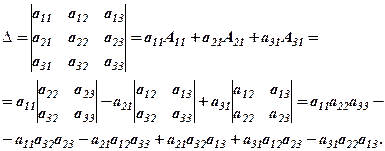
Як бачимо останній вираз збігається з виразом (1) з 1.3.
Рівність типу (1) називають розкладом визначника за елементами першого стовпця.
Вправа. Записати ще 5 розкладів типу (1) для інших рядків і стовпців.
Приклад 2. Обчислити визначник прикладу 1, розкладаючи його за елементами рядків і стовпців.
Розв’язання. Алгебраїчні доповнення вже знайдені у попередньому прикладі, тоді розклади за елементами рядків відповідно запишуться:
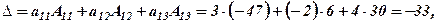
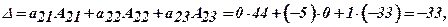
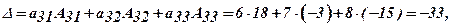 Аналогічні розклади запишемо за рядками:
Аналогічні розклади запишемо за рядками:
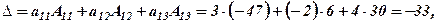
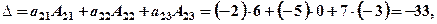
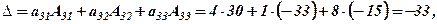 Приклад 3. Обчислити визначник, розклавши його за елементами ІІІ-го рядка
Приклад 3. Обчислити визначник, розклавши його за елементами ІІІ-го рядка
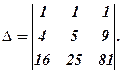
Розв’язання.
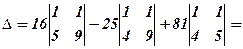
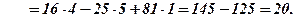 .
.
Приклади. Користуючись теоремою про розклад обчислити визначники: