Электромагнитные колебания и волны
Пример решения задач
1. В колебательном контуре амплитуда колебаний напряжения на обкладках конденсатора за время 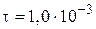 с уменьшается в
с уменьшается в 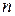 раз (
раз ( 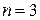 ). Найти: а) величину коэффициента затухания
). Найти: а) величину коэффициента затухания 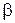 контура; б) величину активного сопротивления
контура; б) величину активного сопротивления 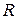 контура; в) добротность
контура; в) добротность 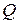 контура, если электроемкость конденсатора
контура, если электроемкость конденсатора 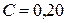 мкФ, индуктивность катушки
мкФ, индуктивность катушки 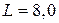 Гн.
Гн.
Дано: 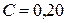 мкФ мкФ 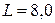 Гн Гн 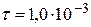 с с 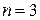 | Решение В колебательном контуре происходят затухающие электрические колебания. Амплитуда колебаний напряжения на обкладках конденсатора 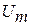 со временем со временем 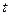 уменьшается по закону уменьшается по закону |
а) 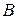 -? б) -? б) 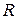 -7 в) -7 в) 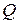 -? -? | 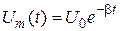 , (1) где , (1) где 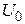 – постоянная величина. – постоянная величина. |
Через промежуток времени 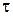 амплитуда напряжения
амплитуда напряжения
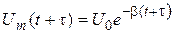 (2)
(2)
и уменьшается в 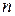 раз. Поэтому из выражений (1) и (2) получается
раз. Поэтому из выражений (1) и (2) получается
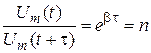 . (3)
. (3)
Прологарифмировав выражение (3), для коэффициента затухания имеем 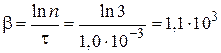 с-1.
с-1.
Коэффициент затухания 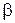 и активное сопротивление
и активное сопротивление 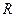 контура связаны соотношением:
контура связаны соотношением:
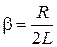 . (4)
. (4)
Отсюда для величины 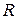 следует:
следует: 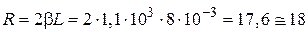 Ом.
Ом.
Как известно, добротность контура определяется формулой:
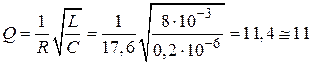
Ответ: а) 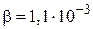 с-1; б)
с-1; б) 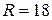 Ом; в)
Ом; в) 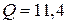
2. Цепь переменного тока частотой 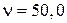 Гц и напряжения
Гц и напряжения 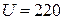 В состоит из последовательно соединенных конденсатора электроемкости
В состоит из последовательно соединенных конденсатора электроемкости 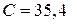 мкФ, катушки индуктивности
мкФ, катушки индуктивности 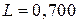 Гн, активного сопротивления
Гн, активного сопротивления 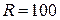 Ом. Найти: а) импеданс (полное сопротивление)
Ом. Найти: а) импеданс (полное сопротивление) 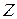 ; б) сдвиг по фазе
; б) сдвиг по фазе 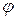 между током и напряжением; в) силу тока
между током и напряжением; в) силу тока 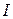 ; г) падение напряжения на конденсаторе
; г) падение напряжения на конденсаторе 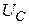 , катушке
, катушке 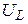 , активном сопротивлении
, активном сопротивлении 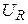 .
.
Дано: 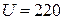 В В 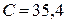 мкФ мкФ 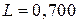 Гн Гн 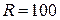 Ом Ом 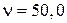 Гц Гц | Решение Величины, характеризующие протекание тока циклической частоты 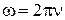 в цепи, определяется выражениями для индуктивного сопротивления в цепи, определяется выражениями для индуктивного сопротивления 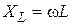 , емкостного сопротивления , емкостного сопротивления 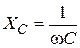 , реактивного сопротивления , реактивного сопротивления 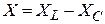 . . |
a) 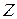 – ? б) – ? б) 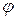 – ? в) – ? в) 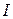 – ? г) – ? г) 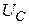 – ? – ? 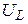 – ? – ? 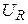 – ? – ? | Поэтому для искомых в задаче величин имеем: а) 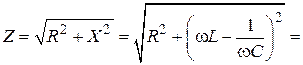 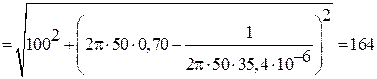 Ом. Ом. |
б) 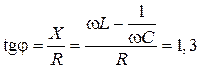 ,
, 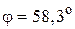 ;
;
в) 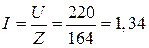 А; г)
А; г) 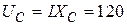 В;
В;
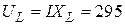 В;
В; 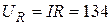 В
В
Ответ: а) 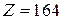 Ом; б)
Ом; б) 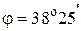 ; в)
; в) 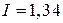 А; г)
А; г) 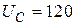 В;
В; 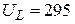 В;
В; 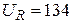 В.
В.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
18. Уравнение изменения силы тока в колебательном контуре дается в виде I = -0,020×sin400 pt (A). Индуктивность контура 1,0 Гн. Найти:
а) период колебаний;
б) емкость контура;
в) максимальную разность потенциалов на обкладках конденсатора.
(T = 5·10-3 c; C = 6,3·10-7 Ф; Umax = 25 B)
19. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре дано в виде
U = 50×сos104pt (В). Емкость конденсатора составляет 9×10-7 Ф. Найти:
а) период колебаний;
б) индуктивность контура;
в) закон изменения со временем силы тока в цепи;
г) длину волны, соответствующую этому контуру.
(T = 2·10-4 c, L = 1,1 мГн, I = -1,4×sin104×pt А, l = 6∙104 м)
20. Колебательный контур состоит из конденсатора ёмкостью С = 7 мкФ, катушки индуктивности L = 0,23 Гн и сопротивления R = 40 Ом. Конденсатор заряжен количеством электричества Q = 5,6×10-4 Кл. Найти:
а) период колебаний контура;
б) логарифмический декремент затухания колебаний.
Написать уравнение зависимости изменения разности потенциалов на обкладках конденсатора от времени.
(T = 8·10-3 c; l = 0,7; U = 80 exp(-87×t)cos(250 pt))
21. В цепь переменного тока напряжением 220 В включены последовательно емкость С, активное сопротивление R и индуктивность L. Найти падение напряжения UR на омическом сопротивлении, если известно, что падение напряжения на конденсаторе равно UC = 2UR и падение напряжения на индуктивности UL = 3UR.
(UR = 156 B)
22. Цепь переменного тока образована последовательно включенными активным сопротивлением R = 800 Ом, индуктивностью L = 1,27 Гн и ёмкостью С = 1,59 мкФ. На зажимы подано 50-периодное действующее напряжение U = 127 В. Найти:
а) действующее значение силы тока I в цепи;
б) сдвиг по фазе между током и напряжением;
в) действующее значение напряжений UR, UL и UC на зажимах каждого элемента цепи.
(71 мА; -63°; 57 В; 28 В; 142 В)
23. Колебательный контур состоит из конденсатора емкостью С = 25 нФ и катушки с индуктивностью L = 1,015 Гн. Обкладкам конденсатора сообщается заряд q = 2,5 мкКл. Написать уравнения (с числовыми коэффициентами) изменения разности потенциалов U и тока I в цепи от времени. Найти разность потенциалов на обкладках конденсатора и ток в цепи в моменты времени T/8, T/4, T/2 (T – период колебаний). Построить графики U(t) и I(t) в пределах одного периода.
( 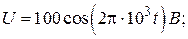
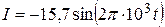 мА;
мА; 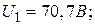
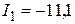 мА;
мА; 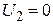 ;
; 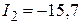 мА;
мА; 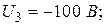
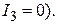
24. В однородной и изотропной среде с 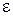 = 3,0 и
= 3,0 и 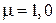 распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны
распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 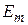 = 10,0 В/м. Найти: а) амплитуду напряженности магнитного поля волны
= 10,0 В/м. Найти: а) амплитуду напряженности магнитного поля волны 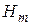 , б)фазовую скорость
, б)фазовую скорость 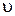 волны.
волны.
( 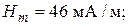
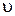 =
= 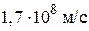 )
)
Оптика
Пример решения задач
1. На мыльную пленку с показателем преломления 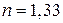 падает по нормали пучок лучей белого света. При какой наименьшей толщине пленки
падает по нормали пучок лучей белого света. При какой наименьшей толщине пленки 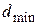 она в отраженном свете будет казаться зеленой (
она в отраженном свете будет казаться зеленой ( 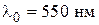 )?
)?
Дано: 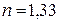 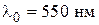 | Решение  |
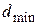 – ? – ? |
Для того, чтобы в отраженном свете пленка выглядела зеленой, необходимо, чтобы при интерференции отраженных лучей выполнялось условие максимума для зеленой части спектра. Оптическая разность хода 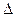 лучей 3 и 2, отраженных от нижней и верхней поверхностей пленки,
лучей 3 и 2, отраженных от нижней и верхней поверхностей пленки,
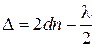 ,
,
(оптический ход в плёнке луча 3 больше луча 2 на 2dn, но луч 2 отражается от оптически более плотной среды, поэтому его ход скачком увеличивается на 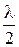 ). Условие максима:
). Условие максима:
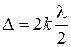 ,
,
где k = 0, 1, 2… . Наименьшая толщина пленки будет при k = 0, тогда
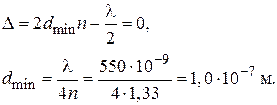
Ответ: 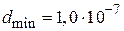 м.
м.
2. На прозрачную дифракционную решетку с периодом 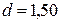 мкм падает нормально монохроматический свет с длинной волны
мкм падает нормально монохроматический свет с длинной волны 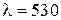 нм. Найти: а) наибольший порядок
нм. Найти: а) наибольший порядок 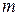 главного дифракционного максимума; б) угол дифракции
главного дифракционного максимума; б) угол дифракции 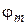 главного дифракционного максимума наибольшего порядка.
главного дифракционного максимума наибольшего порядка.
Дано: 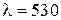 нм нм 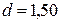 мкм мкм | Решение Условие главного дифракционного максимума порядка 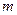 имеет вид имеет вид 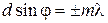 , ( , ( 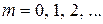 ), ), |
а) 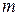 – ? б) – ? б) 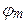 – ? – ? | где 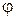 – угол дифракции, соответствующего главного максимума – угол дифракции, соответствующего главного максимума |
Как следует из выпеприведенной формулы, наибольший порядок дифракционного максимума должен удовлетворять соотношению 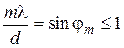 .
.
Отсюда имеем 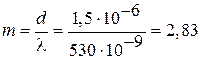 . Поскольку угол
. Поскольку угол 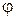 не может быть больше
не может быть больше 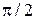 , а m должно быть целым, то выбираем m = 2. Для соответствующего угла дифракции получим
, а m должно быть целым, то выбираем m = 2. Для соответствующего угла дифракции получим 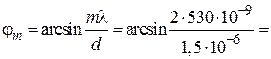 =
= 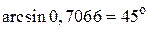
Ответ: а) 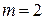 ; б)
; б) 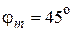
3. Луч света, падающий на поверхность кристалла каменной соли, при отражении максимально поляризуется, если угол падения 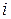 равен 57°. Найти: а) показатель преломления
равен 57°. Найти: а) показатель преломления 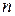 кристалла каменной соли; б) скорость распространения
кристалла каменной соли; б) скорость распространения 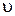 света в этом кристалле.
света в этом кристалле.
Дано: 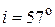 | Решение Согласно закону Брюстера отраженный луч света максимально поляризован, если угол падения луча удовлетворяет соотношению 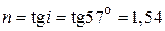 . (1) . (1) |
а) 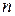 – ? б) – ? б) 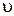 – ? – ? |
Скорость света в кристалле может быть найдена из известного соотношения:
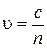 , (2)
, (2)
где 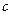 – скорость света в вакуме. Поэтому из формул (1) и (2) имеем
– скорость света в вакуме. Поэтому из формул (1) и (2) имеем
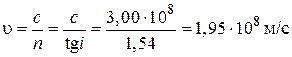 .
.
Ответ: а) 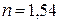 б)
б) 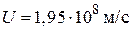
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
25. На мыльную пленку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волны l = 0,60 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина плёнки dmin? (0,11 мкм)
26. Плоская световая волна длиной l0 в вакууме падает по нормали на прозрачную пластинку с показателем преломления n. При каких толщинах b пластинки отраженная волна будет иметь:
а) максимальную интенсивность;
б) минимальную интенсивность?
(а) b = (l0/2n)(m+0,5) (m = 1, 2, 3...); б) b = (l0/2n)m (m = 1,2,3...))
27. Между стеклянной пластинкой и лежащей на ней плоско-выпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус r3 третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны l= 0,6 мкм равен 0,82 мм. Радиус кривизны линзы R = 0,5 м.
28. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l= 500нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin пленки, если показатель преломления материала пленки п = 1,4.
29. Расстояние L от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l = 1 см укладывается N = 10 темных интерференционных полос. Длина волны l = 0,7 мкм.
30. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны l= 500 нм. Найти радиус R линзы, если радиус четвертого, темного Кольца Ньютона в отраженном свете r4 = 2 мм.
31. На тонкую глицериновую пленку толщиной d=1,5 мкм нормально к ее поверхности падает белый свет. Определить длины волн l, лучей видимого участка cпектра (0,4 ≤ l ≤ 0,8 мкм), которые будут 'ослаблены в результате интерференции.
32. На стеклянную пластину нанесен тонкий слой прозрачного вещества с показателем преломления п = 1,3. Пластинка освещена параллельным пучком Монохроматического света с длиной волны l = 640 нм, падающим на пластинку нормально. Какую минимальную толщину должен иметь слой, чтобы отраженный пучок имел наименьшую яркость?
33. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны l = 500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете b= 0,5 мм. Определить угол a между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, n = 1,6.
34. Плосковыпуклая стеклянная линза с f = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете r5 = 1,1 мм. Определить длину световой волны l .
35. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (l=590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d3 воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо.
|
Красная линия (l = 6300 Å) видна в спектре 3-го порядка под углом j = 60°. Определить: а) какая спектральная линия видна под этим же углом в спектре 4-го порядка; б) какое число штрихов на 1 мм длины имеет дифракционная решетка.
(l = 475 нм; N = 460 мм-1)
37. Источник света диаметром d = 30,0 см находится от места наблюдателя на расстоянии l = 200 м. В излучении источника содержатся волны длиной от 490 до 510 нм. Оценить для этого излучения: а) время когерентности 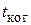 ; б) длину когерентности
; б) длину когерентности 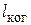 ; в) радиус когерентности
; в) радиус когерентности 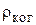 .
.
( 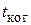
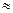
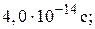
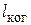
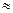 0,010 мм;
0,010 мм; 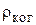
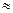 0,30 мм)
0,30 мм)
38. Какое наименьшее число Nmin штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн l1=589,0 нм и l2= 589,6 нм? Какова длина l такой решетки, если постоянна решетки d = 5 мкм?
39. На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в п = 4,6 раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теорети- чески можно наблюдать в данном случае.
40. На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница (l =780 нм) спектра третьего порядка?
41. На дифракционную решетку, содержащую п = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется поме- щенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L=1,2 м. Границы видимого спектра: l кр=780 нм, lф=400 нм.
42. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние d между атомными плоскостями равно 280 пм. Под углом q = 65° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны l рентгеновского излучения.
43. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (l=600 нм).Угол отклонения лучей, соответствующих второму дифракционному максимуму, j = 20°. Определить ширину а щели.
44. На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Dj = 16°. Определить длину волны l света, падающего на решетку.
45. На дифракционную решетку падает нормально монохромати- ческий свет (l=410 нм). Угол Dj между направлениями на максимумы первого и второго порядков равен 2°2/. Определить число п штрихов на 1 мм дифракционной решетки.
46. Постоянная дифракционной решетки в п = 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол a между двумя первыми симметричными дифракционными максимумами.
47. Расстояние между штрихами дифракционной решетки d=4 мкм. На решетку падает нормально свет с длиной волны l = 0,58 мкм. Максимум какого наибольшего порядка дает эта решетка?
48. Пластина кварца толщиной d1 = 1,0 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол j1 = 20°. Определить:
а) какова должна быть длина d2 кварцевой пластинки, помещенной между двумя “параллельными” николями, чтобы свет был полностью погашен;
б) какой длины l трубку с раствором сахара концентрации С = 0,40 кг/л надо поместить между николями для получения того же эффекта.
Удельное вращение раствора сахара a0 = 0,665 град/(м-2×кг).
(d2 = 4,5 мм; l = 3,4 дм)
49. Под каким углом к горизонту должно находиться солнце, чтобы его лучи, отраженные от поверхности озера, стали бы наиболее полно поляризованы, если скорость света в воде 2,26×108 м/с? (37°)
50. Пластинка кварца толщиной d = 4,0 мм (удельное вращение кварца 15 град/мм), вырезанная перпендикулярно оптической оси, помещена между двумя скрещенными николями. Пренебрегая потерями света в николях, определите, во сколько раз уменьшится интенсивность света, прошедшего эту систему.
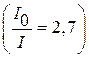 .
.
