Релятивистский закон преобразования скоростей

Преобразования Лоренцанетрудно обобщить на случай произвольной взаимной ориентации систем 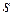и , и 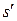произвольного направления скорости 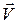. Для этого заметим, что при переходе от одной ИСО к другой, преобразуется только продольная компонента 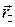радиус- вектора 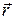, а поперечная 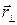не преобразуется. Разложение 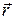на продольную и поперечную 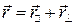удобно осуществлять с помощью проективных операторов

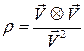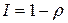, (7)

со следующими свойствами:

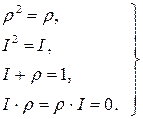(8)

Оператор 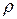позволяет находить проекцию 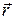на направление, задаваемое вектором 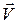, а оператор I - на ортогональную ему плоскость, так что

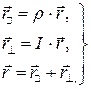(9)

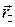и и 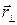преобразуются при переходе от s к 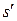следующим образом:

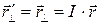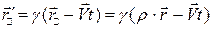, , (10)

а

.

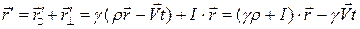Итак,

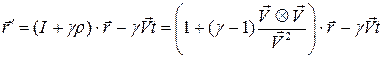. (11)

Для 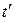будем иметь

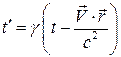. (12)

Обратные преобразования получаются заменой штрихованных величин на не штрихованные, а V на -V .

Закон преобразования скорости легко найти, вычисляя дифференциалы от левой и правой частей соотношений (11)-(12) :

то .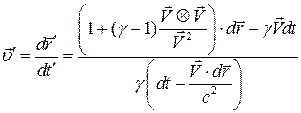

Таким образом,

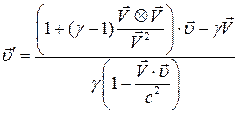, (13)

Обратное преобразование имеет вид

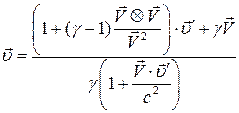. (14)

В частном случае, когда 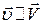, получаем

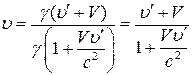. (15)

Соотношения (13)-(15) выражают релятивистский закон сложения скоростей. Формулу (15) называют формулой Эйнштейна.