Тема 5: решение нелинейных уравнений и систем

Цель работы: Изучение возможностей пакета Ms Excel при решении нелинейных уравнений и систем. Приобретение навыков решения нелинейных уравнений и систем средствами пакета.

Решение нелинейных уравнений.

ПРИМЕР 5.1. Найти корни полинома .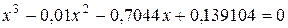

Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x,при котором функция обращается в ноль.

Проведем табулирование полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на рис. 5.1., где в ячейку В2 была введена формула: =A2^3-0,01*A2^2-0,7044*A2+0,139104.На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].

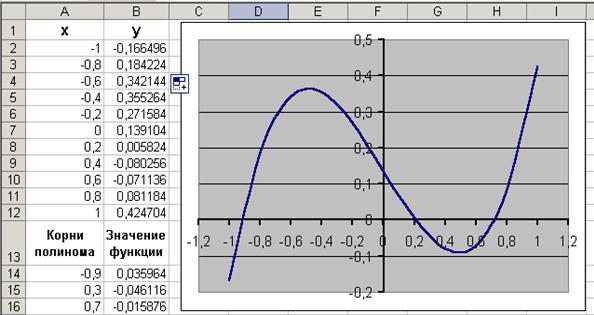
Рис. 5.1

Теперь можно найти корни полинома методом последовательных приближений с помощью команды Сервис®Подбор параметра. Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис®Параметры.

В качестве начальных значений приближений к корням можно взять любые точки из отрезков локализации корней. Пусть это будут -0.9, 0.3 и 0.7. Введем эти значения в диапазон А14:А16, а в ячейку В14 (рис. 5.1) введем формулу: =A14^3-0,01*A14^2-0,7044*A14+0,139104, которую скопируем в ячейки В15 и В16 при помощи маркера заполнения.

После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис®Подбор параметраи заполнить диалоговое окно следующим образом (рис. 5.2).

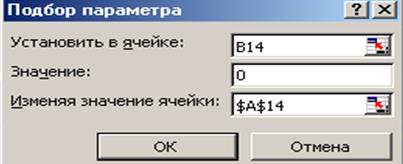
Рис. 5.2

В поле Установить в ячейке дается ссылка на ячейку в которую введена формула, вычисляющая значение левой части уравнения (уравнение должно быть записано так, чтобы его правая часть не содержала переменную). В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке.

После нажатия кнопки ОКпоявится диалоговое окноРезультат подбора параметра (рис. 5.3) с сообщением об успешном завершении поиска решения и приближенное значение корня будет помещено в ячейку А14.

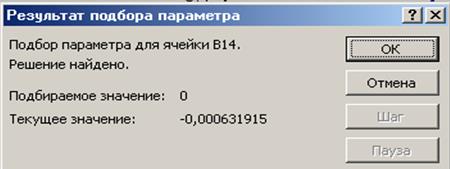
Рис. 5.3

Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16 (рис. 5.4).

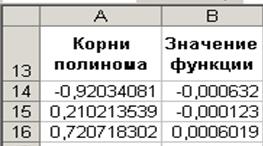
Рис. 5.4

ПРИМЕР 5.2. Решить уравнение .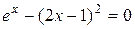

Проведем локализацию корней нелинейного уравнения.

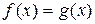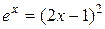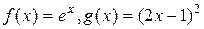Для этого представим его в виде , т.е. или , и решим графически.

Графическим решением уравнения 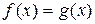будет точка пересечения линий 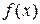и .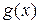

Построим график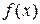и и 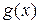. Для этого в диапазон А3:А18 введем значения аргумента. В ячейку В3 введем формулу для вычисления значений функции 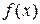: =EXP(A3), а в С3 для вычисления 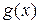: =(2*A3-1)^2.

Результатывычисленийи построение графиков 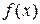и 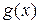в одной графической области (см ПРИМЕР 3.5 и 3.6) показаны на рис. 5.5.

На графике видно, что лини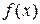и и 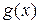пересекаются дважды, т.е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно:

.

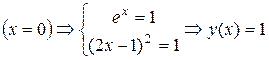Для второго можно определить интервал изоляции корня: .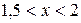

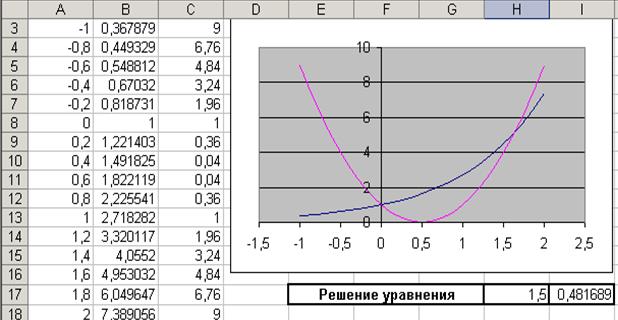
Рис. 5.5

Теперь можно найти корень уравнения на отрезке [1.5,2] методом последовательных приближений.

Введём начальное приближение в ячейку Н17=1,5, и само уравнение, со ссылкой на начальное приближение, в ячейку I17 =EXP(H17)-(2*H17-1)^2 (рис. 6.5).

Далее воспользуемся пунктом меню Сервис®Подбор параметраи заполним диалоговое окно Подбор параметра (рис.5.6).

Результатпоиска решения будет выведен в ячейкуН17(рис. 5.7).

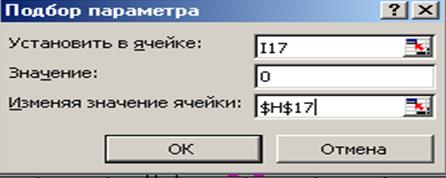
Рис. 5.6

Рис. 5.7

Решение систем уравнений.