Розв’язання. Спочатку складемо рівняння прямої , яка проходить через точку перпендикулярно даній прямій (Рис.39.3)

Накреслимо рисунок.

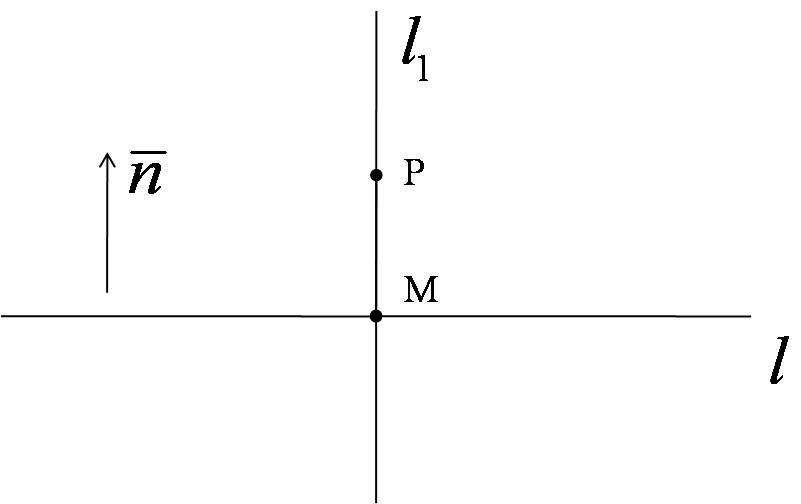
Рис. 39.3

Спочатку складемо рівняння прямої 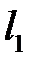, яка проходить через точку 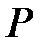перпендикулярно даній прямій (Рис.39.3). Нормальним вектором для даної прямої є вектор 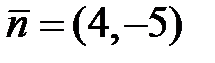, і цей вектор є напрямним для прямої 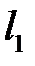. Тому канонічне рівняння прямої :

.

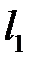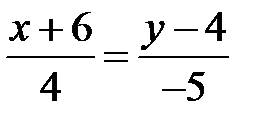В результаті перетворень це рівняння набуде вигляду.

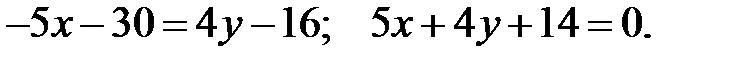
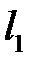Шукана точка М є точкою перетину та , тому її координати знайдемо, розв’язавши систему:

.

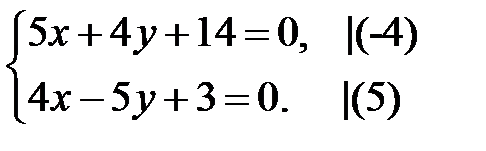Маємо

.

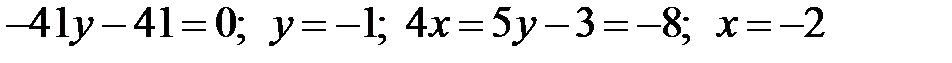Отже, координати точки .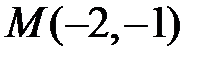

Задача 39.8.Дано рівняння двох сторін прямокутника 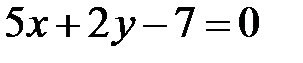, 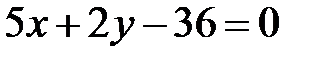та рівняння його діагоналі 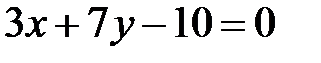. Скласти рівняння інших двох сторін цього прямокутника.

Розв’язання. Відразу помітимо, що дві задані прямі паралельні, оскільки мають однакові нормальні вектори, тому представляють протилежні сторони прямокутника, наприклад 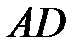і .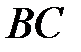

Точка 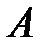є точкою перетину 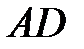і діагоналі 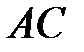, тому знайдемо її координати, розв’язавши систему рівнянь.

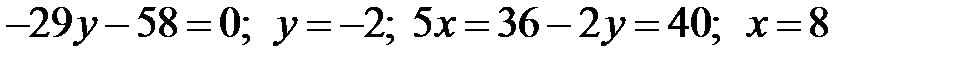, тобто .

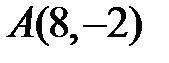Аналогічно знайдемо точку , як точку перетину 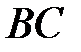та діагоналі .

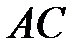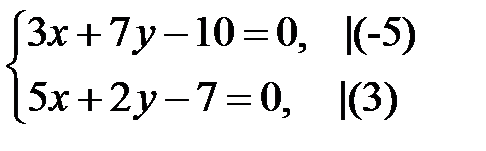
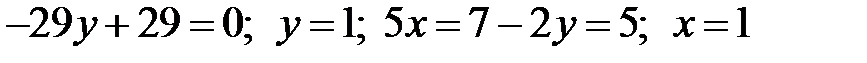, тобто .

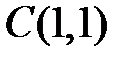Нормальним вектором для 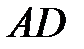і 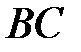є вектор 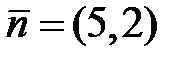. Цей вектор є напрямним для 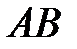і 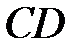. Тому рівняння цих сторін такі:

;

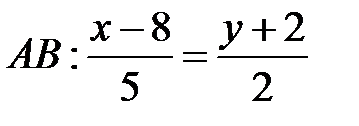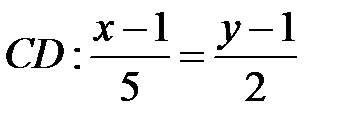
Задача 39.9.Знайти кут між прямими 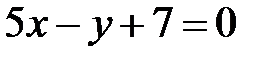та 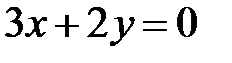.