Iii. примеры решения задач

Требования к оформлению решения задачи:

1. Изучить условие и ввести буквенные обозначения величин (если их нет в условии), сделать краткую запись условия;

2. Перевести данные в СИ или обосновать, почему такой перевод нецелесообразен;

3. Построить чертеж (график, схему соединений, схему установки и пр.) в подходящем масштабе. На чертеже проставить обозначения используемых (введенных) величин. На графиках оси координат обозначать стрелками (возможно, с разрывами и изменением масштаба), а также обязательно проставить обозначение и через запятую - наименование физической величины. При необходимости следует выделять фрагмент чертежа в отдельный чертеж, рисунок, схему;

4. Указать используемые физические законы и дать их математическое выражение (формулы). Все символы должны быть расшифрованы с указанием физической величины, единицы измерения и размерности;

5. Решить задачу в общем виде (в виде уравнения, системы уравнений и пр., которые включают в себя как искомые, так и заданные (введенные, табличные) величины). Вывести рабочую формулу. Нумерация формул производится по правому краю строки в круглых скобках;

6. Проанализировать это решение на предмет выявления избыточных данных;

7. По рабочей формуле проверить размерность искомой физической величины;

8. Определить необходимую для расчета точность задания данных и произвести расчет по рабочей формуле;

9. Проанализировать полученный результат с точки зрения его реальности (соответствия здравому смыслу), а именно, сравнить его с табличными значениями, с другими аналогичными результатами, выполнить предельные переходы;

10. Результат решения задачи записывать отдельной строкой, начиная со слова «Ответ: ». В ответе привести найденное значение физической величины с нужной точностью, а также указать ее наименование.

Оценка решения (по десятибалльной шкале):

1. Полное количество баллов ставится тогда, когда:

- правильно выполнены необходимые чертежи (рисунки), поясняющие содержание и ход решения задачи;

- данные задачи приведены в одну систему единиц (желательно в СИ),

- верны исходные формулы и задача решена в общем виде; в окончательную формулу подставлены числовые данные и получен правильный ответ;

- решение во всех частях оформлено аккуратно.

2. Баллы снимаются в следующих случаях:

- до 5 баллов – за отсутствие пояснения хода решения задачи;

- до 5 баллов – за отсутствие чертежа (рисунка) поясняющего содержание и ход решения задачи или небрежное оформление правильно решенной задачи;

- до 5 баллов – за отсутствие решения в общем виде;

- до 5 баллов – за ошибки при переводе величин в одну систему единиц (СИ) или ошибки в промежуточных расчетах при правильных исходных формулах и верном ходе решения.

Рассмотрим конкретный пример решения и оформления задачи.

Плоская монохроматическая волна ( l = 0.60 мкм ) падает на диафрагму с узкой щелью ширины b = 0.04 мм. За щелью находится собирающая линза ( f = 40 см), в фокальной плоскости которой расположен экран для наблюдения интерференции. Определить положение минимумов первого и второго порядков на экране и относительную интенсивность первого максимума.

Прежде, чем начать решать задачу, необходимо четко уяснить физический смысл задачи и тех вопросов, которые поставлены в ней. Для облегчения решения задачи и повышения ее наглядности необходимо, если это возможно, представить (оптическую) схему установки.

Как правило, решение задачи надо искать вначале в общем виде, получая выражение искомой физической величины через другие, приводимые в условии задачи. На этом этапе можно оценить правильность решения по размерности и характеру полученной зависимости (по поведению решения в характерных точках).

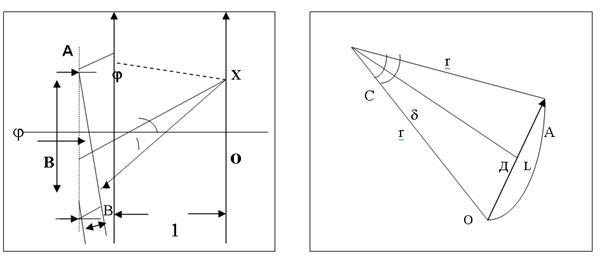
Анализ условия задачи. Как следует из описания установки, наблюдается дифракция в параллельных лучах (дифракция Фраунгофера). Оптическая схема строится так, что в каждую фиксированную точку экрана приходят волны, которые после щели образуют плоский фронт, повернутый по отношению к фронту падающей волны на некоторый угол j (j - угол дифракции). В падающей волне колебания во всех точках фронта происходят в одинаковой фазе. Вдоль фронта дифрагированой волны фаза от точки к точке изменяется, и, например, для точек А и В (см. рис.) разность фаз равна

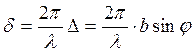(1)

Интенсивность в той или иной точке экрана, а, следовательно, положение минимумов и максимумов на экране можно найти по принципу Гюйгенса – Френеля, как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели, с учетом разности фаз вторичных волн.

Проще всего провести геометрическое сложение колебаний, приходящих в некоторую точку экрана. Для этого разобьем щель на Z очень узких элементарных полосок ширины Db каждая. При достаточно малых значениях Db можно считать, что все вторичные источники одной элементарной полоски изучают волны, которые при заданном угле j подходят к линзе без разности хода, т.е. без разности фаз. Поскольку тонкая линза не изменяет фазы проходящих через нее волн, то такие волны придут к соответствующей точке экрана так же без сдвига по фазе.

Обозначим d_i - разность фаз между волнами от двух соседних элементарных полосок, а_i - амплитуда результирующей волны, излучаемой одной полоской. Очевидно, результат векторного сложения будет тем точнее, чем меньше ширина Db каждой элементарной полоски и, соответственно, чем больше число Z таких полосок. В пределе при Db®O число z® 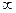. В этом случае z® .

,

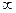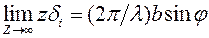где d - разность фаз между волнами, излучаемыми вторичными источниками, расположенными по краям щели. Предел.

lim z a_i =A₀,

где A₀ -результирующая амплитуда колебаний, которая имела бы место, если бы волны от всех вторичных источников приходили в некоторую точку экрана без разности фаз.

В данной схеме такой точкой является точка 0, совпадающая с главным фокусом линзы. В точке 0 собираются лучи, параллельные оптической оси линзы, для которой угол дифракции j = 0.

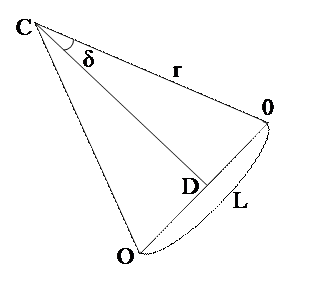
При векторном сложении колебания от отдельных элементарных полосок представляются векторами разной длины. Но из–за cдвига фаз такие векторы повернуты один относительно другого на один и тот же угол d_i, образуя звенья правильной ломаной линии. Когда каждый из векторов стремится к нулю, получим плавную кривую, имеющую форму дуги окружности, ее длина L = A₀, где А₀ - результирующая амплитуда в точке 0 экрана (рис.). Соответствующий этой дуге центральный угол равен d. Искомая амплитуда А_j -хорда, стягивающая эту дугу.

Для расчета А_d рассмотрим D СОД . Очевидно,

ОД = А_j /2 = r sin( d/2 )

Радиус окружности

r = L/d .Тогда А_j = А₀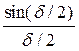

Учитывая, что интенсивность I » A_j² , получим:

Á = Á₀ sin² (d/2)/ (d/2)² , (2)

где

Á₀ » A₀² - интенсивность центрального максимума.

Как следует из выражения (2), Á = 0, если sin(d/2)= 0

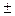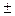т.е d/2 = mp, где m = I, 2, 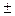3, … , или d = 2mp.

Учитывая выражение (1) получим условие минимумов:

b sinj = ml (3)

Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются из решения трансцендентного уравнения tg d/2 = d/2. Практически можно считать, что максимумы располагаются посередине между соседними минимумами, т.е. положение максимумов определяется приближенным условием

b sinj = (2к + 1)l/2 (4)

Решение.

В точку х = 0 — главный фокус линзы — приходят лучи, идущие под углом j = 0, т.е. в этой точке наблюдается центральный максимум. Координата любой точки на экране, в которую приходят лучи, связана с углом дифракции j следующим образом:

х = f tgj (5)

Для минимумов 1-ого и 2-ого порядков угол j удовлетворяет условию (3) (m₁ = 1 и m₂ = 2)

Полученные значения синусов настолько малы, что можно считать sinj = tgj. Тогда по формуле (5) имеем координаты минимумов 1-го и 2-ого порядков

х₁ = 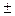6 мм и х₂ = 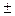12 мм.

Положение максимумов первого порядка также может быть определено из равенств (5) и (4) при к = 1

sinj/1 = 3l / (2b) x/1 = 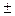9 мм

Чтобы определить относительную интенсивность первого максимума, используем выражение (2). Подставив условие (4) При к = 1 в (1) получим d = 3p, откуда (см. (2))

Á₁ / Á₀ = 4 / (9p²) » 0,045.

Ответ: х₁ = 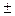6 мм и х₂ = 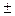12 мм. Á₁ / Á₀ » 0,045