Вычисление бесконечных сумм с заданной точностью

Лабораторная работа 5.

Оглавление

1. Вычисление конечных сумм и произведений. 2

2. Использование рекуррентных соотношений. 2

3. Вычисление бесконечных сумм с заданной точностью.. 3

4. Задания. Вычисление сумм и произведений. 4

5. Задания. Использование рекуррентных формул. 5

6. Задания. Вычисление бесконечных сумм.. 9

7. Практикум.. 13

Вычисление конечных сумм и произведений

Вычисление конечных сумм и произведений - это наиболее часто встречающийся тип элементарных задач (см. также лабораторную работу 1). Пусть требуется вычислить сумму вида

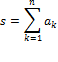
Для вычисления суммы можно применить следующий алгоритм:

//Инициализация переменных. Подготовительные вычисления. . .s=0;for(int k=1; k<=n; k++){ //Вычислить текущий член суммы ak … s+=ak;}

Если при вычислении текущего слагаемого a_k (внутри цикла) выполняются операции, не зависящие от k, эти вычисления целесообразно вынести из цикла for() и выполнить их один раз перед циклом. Например, пусть требуется вычислить сумму вида

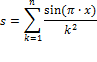
Соответствующий код может быть следующим:

//Инициализация переменных. Подготовительные вычисленияdouble ak=0, sx=Math.Sin(Math.PI*x);s=0;for(int k=1; k<=n; k++){ //Вычислить текущий член суммы ak ak=sx/(k*k); s+=ak;}

Использование рекуррентных соотношений

Вернемся к задаче из лабораторной работы 1. Пусть требуется вычислить сумму вида

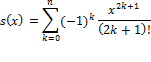
Здесь вычисление текущего члена суммы можно значительно упростить (и уменьшить количество операций), если для вычисления текущего слагаемого построить и использовать рекуррентную формулу вида

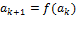
Такую формулу можно получить следующим образом. Выпишем сначала выражения для к-го и к+1-го слагаемого

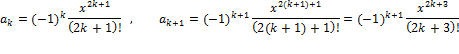
Поделив к+1-е слагаемое на к-е слагаемое, получим рекуррентную формулу

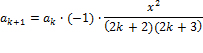
Причем при k=0 имеем

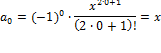
алгоритм вычисления суммы с использованием рекуррентной формулы можно записать в виде

//Инициализация переменных. Подготовительные вычисления//Предполагается, что значения переменных x и n определены ранее//ak первоначально полагаем равным a₀double ak=x, dx=x*x;S=ak;for(int k=1; k<=n; k++){ //Вычислить текущий член суммы ak, используя рекуррентную формулу ak*=-dx/(2*k+2)/(2*k+3); S+=ak;}

Вычисление бесконечных сумм с заданной точностью

Пусть теперь требуется вычислить сумму вида

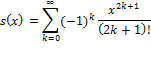
с заданной точностью e>0 (некоторое малое число). Под этим подразумевается, что очередные слагаемые a_k нужно добавлять к текущему значению s(x), пока они достаточно большие по модулю, т.е. удовлетворяют условию

|a_k|>e

Поскольку в этом случае число слагаемых заранее неизвестно, для суммирования можно использовать циклы типа while() или do-while(). Предыдущий алгоритм суммирования модифицируется следующим образом

//Инициализация переменных. Подготовительные вычисления//Предполагается, что значения переменных x, n и точность eps//определены ранее//ak первоначально полагаем равным a₀ double ak=x, dx=x*x;int k=0;S=0;While(Math.Abs(ak)>eps){ S+=ak; //Вычислить следующий член суммы ak, используя рекуррентную формулу k++; ak*=-dx/(2*k+2)/(2*k+3);}