Теоремы сложения и умножения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е., если 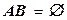, то P(A+B) = P(A) + P(B).

В общем случае вероятность суммы двух событий вычисляется по формуле

P(A+B) = P(A) + P(B) – P(AB).

Вероятность противоположного события .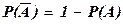

Условная вероятность 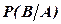события В при условии, что событие А произошло, определяется формулой 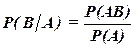, где P(A) ¹ 0.

Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого, при условии, что первое событие наступило .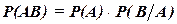

Если события А и Внезависимы, т.е. появление одного из них не меняет вероятности появления другого, то .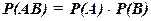

Для нахождения вероятности суммы независимых событий 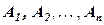целесообразно переходить к противоположным событиям:

.

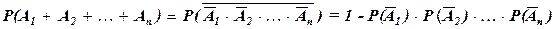4.1. Производится один выстрел по круговой мишени, состоящей из круга и двух концентрических колец. Вероятности попадания при одном выстреле в круг и кольца соответственно равны 0,12, 0,22, 0,38. Найти вероятность промаха.

4.2. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплёте. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплёте.

4.3. Станок штампует детали. Вероятность того, что за смену не будет выпущено ни одной нестандартной детали, равна 0,85. Найти вероятность того, что за три смены не будет выпущено ни одной нестандартной детали.

4.4. Производится независимый пуск двух ракет по цели. Найти вероятность поражения цели, если первая ракета поражает цель с вероятностью 0,6, а вторая – 0,8.

4.5. Вероятность попадания в мишень при одном выстреле равна 0,8. Стрелок произвёл три независимых выстрела. Найти вероятность того, что в мишени будет: а) три попадания, б) хотя бы одно попадание, в) только два попадания.

4.6. Бросают два игральных кубика. Рассмотрим события: А – только одно из чисел на верхних гранях больше 3, В – сумма чисел на верхних гранях кратна 3. Будут ли независимыми события А и В?

4.7. Изготовлено 30 подшипников, причём 5 из них соответствуют размерам III группы ГОСТа, 10 – II группы ГОСТа, остальные – I группы ГОСТа. Какова вероятность того, что первый отобранный на сборку подшипник будет принадлежать III группе, второй – II группе и третий – I группе?

4.8. В каждом из трёх ящиков находятся 1 белый и 2 красных шара. Из первого ящика случайным образом выбирают один шар и перекладывают его во второй ящик. Затем из второго ящика наудачу перекладывают один шар в третий ящик. Какова вероятность того, что в третьем ящике станет 2 белых шара?

4.9. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго эта вероятность равна 0,8.

4.10. Гардеробщица выдала одновременно номерки четырём мужчинам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятности следующих событий: А – каждому из четырёх мужчин гардеробщица выдаст его собственную шляпу, В – трое мужчин получат свои шляпы, С – двое мужчин получат свои шляпы, D – один мужчина получит свою шляпу, Е – ни один из четырёх мужчин не получит своей шляпы.

4.11. От коллектива, который состоит из 6 мужчин и 4 женщин, на конференцию выбираются 2 человека. Какова вероятность того, что среди выбранных будет хотя бы одна женщина.

4.12. В первом ящике находятся 7 белых и 3 чёрных шара, а во втором –
2 белых и 3 чёрных шара. Из первого ящика случайным образом выбирают один шар и перекладывают его во второй ящик. Затем из второго ящика наудачу перекладывают один шар в первый ящик. Найти вероятность того, что число белых шаров во втором ящике не изменится.

4.13. Студент пришёл на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачёт, если после отказа отвечать на вопрос преподаватель задаёт ещё один вопрос?

4.14. Вероятность хотя бы одного попадания в цель при четырёх выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

4.15. Детали могут быть изготовлены с применением двух технологий. В первом случае деталь проходит три технические операции, вероятности получения брака при каждой из которых равны соответственно 0,01, 0,2, 0,3. Во втором случае имеются две операции, вероятности получения брака при каждой из которых одинаковы и равны 0,3. При первой технологии вероятность получения из доброкачественной детали изделия первого сорта равна 0,9, при второй – 0,8. Определить какая технология обеспечивает большую вероятность получения первосортной продукции.