Замена дискретной системы эквивалентной непрерывной системой

В случае дискретных систем с коррекцией на входе непрерывной части (см. рис. 1.50) структурную схему сводят к эквивалентной непрерывной схеме на основании следующих преобразований

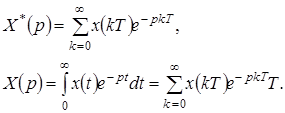(1.62)

Моделью идеального импульсного элемента (ИИЭ) можно считать

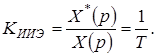(1.63)

Для экстраполятора нулевого порядка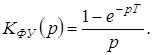

Согласно выражению (1.34), .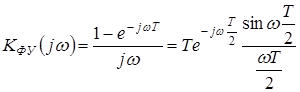

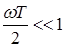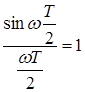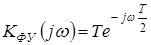Если , то , и передаточная функция импульсного элемента

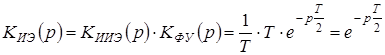. (1.64)

Таким образом, реальный импульсный элемент с устройством хранения информации вносит запаздывание, равное 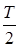. Преобразованная таким образом структурная схема показана на рис. 1.51.

На практике при моделировании применяют более точное выражение

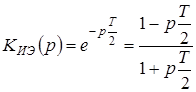. (1.65)

Как следует из (1.65), эта передаточная функция соответствует неминимально-фазовому звену.

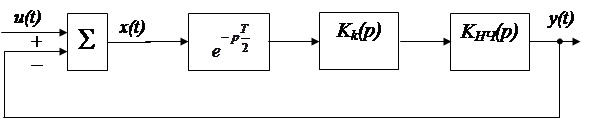Рис. 1.51. Преобразованная структурная схема дискретной системы

При принятии решения о замене дискретной системы эквивалентной непрерывной системой необходимо сравнить значение периода дискретизации Т с рядом величин, влияющих на процессы в системе. Эквивалентирование возможно при выполнении ряда условий:

1. 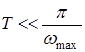, где 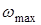– наибольшая частота возмущающих и задающих сигналов. Обычно принимают .

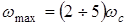2. 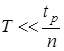, где 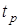– время регулирования, а п – порядок системы.

3. В следящих системах с учетом динамической точности 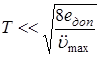, где 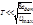– заданная ошибка слежения, 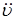– максимальное ускорение входного сигнала.

4. С учетом ухудшения запаса устойчивости 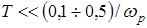, где 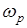– рабочая частота сигналов в системе.

5. С учетом показателя колебательности .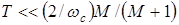

Из всех ограничений выбирают наиболее жесткое.

После этого осуществляется расчет коррекции методами непрерывных систем. Правильность выбора величины периода дискретизации подтверждается результатами компьютерного моделирования системы.

Пример.

Оценить влияние величины периода дискретизации Т на процессы в системе путем моделирования на ПЭВМ [5]. Структура скорректированной системы приведена на рис. 1.52. Схема моделирования в Simulink – на рис. 1.53.

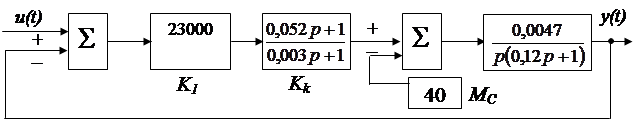Рис. 1.52. Структурная схема скорректированной дискретной системы

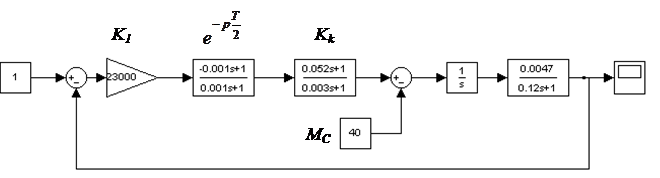
Рис. 1.53. Схема моделирования скорректированной дискретной системы

В результате исследования системы при Т = 0,002 с кривые переходного процесса в непрерывной системе (без элемента 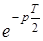) и с учетом дискретизации (при наличии 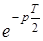) практически совпали (рис. 1.54). При Т » 0,01 с в системе значительно возрастает перерегулирование (рис. 1.55, а), а при Т = 0,03 – процесс колебательный, расходящийся (рис. 1.55, б).

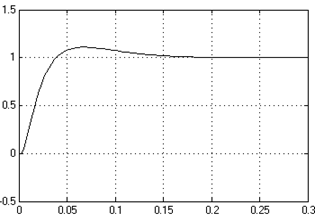
Рис. 1.54. Переходной процесс в непрерывной и в дискретной системе

при Т = 0,002 с

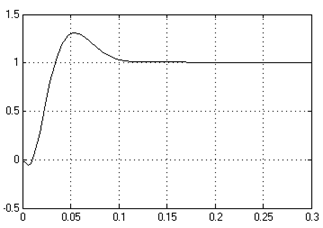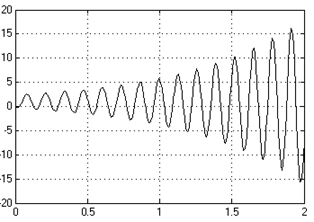Рис. 1.55. Переходные процессы в дискретной системе:

а – при Т = 0,01 с; б – при Т = 0,03 с

Величина Т = 0,002 с соответствует условию 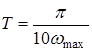, где 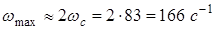. В данной системе частота среза .

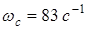Цифровые ПИД-регуляторы

Рассмотрим последовательность синтеза корректирующего устройства дискретной системы в виде ПИД-регулятора.

Если непрерывный ПИД-регулятор описывается передаточной функцией

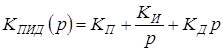(1.66)

и непрерывным уравнением 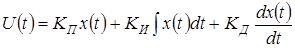, то цифровой ПИД-регулятор описывается дискретной передаточной функцией и разностным уравнением. Получим дискретную передаточную функцию интегратора, который описывается уравнением

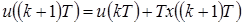, (1.67)

что соответствует правилу прямоугольников (метод Эйлера) численного интегрирования.

Применив к уравнению (1.67) z–преобразование, получим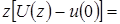

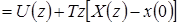, а при нулевых начальных условиях

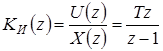. (1.68)

Дифференцирование описывается разностным уравнением

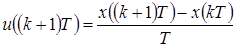, (1.69)

а передаточная функция будет иметь вид

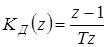. (1.70)

Объединяя передаточные функции пропорционального, интегрирующего и дифференцирующего звеньев, получим передаточную функцию цифрового ПИД-регулятора

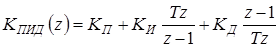. (1.71)

Этой передаточной функции соответствует разностное уравнение

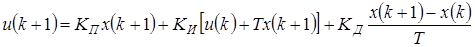. (1.72)

Пример.

Пусть при коррекции непрерывной системы получен ПИД-регулятор с передаточной функцией 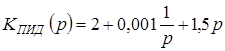. Необходимо записать передаточную функцию дискретного регулятора с периодом дискретизации Т = 0,01 с.

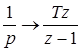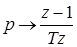Так как , а , то 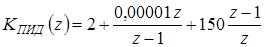.