Основные параметры состояния, их измерение

Любое вещество может находиться в одном из трех состояний: в виде газа, жидкости или твердого тела. При заданных условиях рассматриваемое вещество всегда находится лишь в одном неизменном состоянии. Например, в условиях окружающей человека среды воздух находится в газообразном состоянии. Изменяя эти условия, его можно превратить в жидкость или твердое тело.

Для того чтобы однозначно определить состояние рассматриваемого вещества, вводятся характеристики, называемые параметрами состояния. Параметры, которые можно измерить, называются основными: абсолютное давление, абсолютная температура, удельный объем.

Абсолютное давление р представляет собой силу, действующую по нормали к поверхности тела и отнесенную к единице этой поверхности. Возникновение этой силы связано с ударными воздействиями множества молекул на граничные стенки. Величина давления зависит от концентрации и подвижности молекул. Абсолютное давление обычно подсчитывается по показаниям двух приборов. В точке 1 (рис. 1.1) абсолютное давление р₁ выше атмосферного давления р_б, измеряемого барометром, на величину избыточного давления р_м, измеряемого манометром. Для этой точки

р₁ = р_б + р_м, (1.1)

т. е. при давлениях р, больших атмосферного, абсолютное давление складывается из избыточного и атмосферного и определяется по показаниям манометра и барометра. В точке 2, лежащей ниже линии атмосферного давления,

р₂ = р_б ­– р_в, (1.2)

где р_в – показание вакуумметра, служащего для измерения разрежения. Таким образом, если абсолютное давление меньше атмосферного, то оно равно разности показаний барометра и вакуумметра.

Единицей измерения давления в Международной системе единиц СИ, введенной в нашей стране с января 1963 г. в качестве предпочтительной, является паскаль (Па). 1 Па – давление, оказываемое силой 1 Н (ньютон) на нормальную поверхность площадью 1 м², т. е. 1 Па = 1 Н/1м².

Так как величина этой единицы очень мала, то для практических измерений применяют кило-паскаль (1 кПа = 10³ Па) и мегапаскаль (1 МПа =
= 10⁶ Па). Встречается также единица, близкая по величине к атмосферному давлению, – бар (1 бар =
= 10⁵ Па = 10⁵ Н/м²).

В практике находят применение и другие единицы измерения давления: техническая атмосфера
(1 ат = 1 кгс/см²), физическая атмосфера (1 атм =
= 760 мм рт. ст.), миллиметр ртутного или водяного столба. В табл. 1.1 приводятся соотношения между различными единицами измерения давления.

Температура характеризует тепловое состояние тела, степень его нагрева. Единицей термодинамической температуры является кельвин (К), представляющий собой 1/273,16 часть интервала от абсолютного нуля до температуры тройной точки воды.

Таблица 1.1

Соотношения между единицами измерения давления

Единица измерения	Па	бар	ат	атм	мм рт. ст.
Па		10-5	1,01972∙10-5	0,986223∙10-5	750 ∙10-5
бар	105		1,01972	0,986223	750,062
ат		0,980665		0,96784 1	735,550
атм		1,01325	1 ,03323		760,00
мм рт. ст.	133,3	1,333∙10-3	1,359∙10-3	1,316∙10-3

Тройная точка воды – это температура, при которой все три фазы воды (твердая, жидкая и газообразная) находятся в равновесии; она равна 273,16 K. Температура таяния льда на 0,01 меньше температуры тройной точки и равна 273,15 K.

За параметр состояния рабочего вещества в термодинамике принимают абсолютную термодинамическую температуру Т, измеряемую в кельвинах. В практических измерениях находит применение шкала Цельсия, цена деления которой равна цене деления абсолютной шкалы, однако за начало отсчета принят не абсолютный нуль, а точка таяния льда. Температура, измеренная в градусах Цельсия, обозначается t и связана с Т формулой:

t = T – 273,15. (1.3)

Удельный объем v вещества представляет собой объем единицы массы вещества. Если V – объем (м³), занимаемый телом массой М кг, то удельный объем, м³/кг,

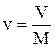. (1.4)

Величина, обратная удельному объему, называется плотностью вещества, кг/м³:

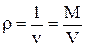. (1.5)

Объем, занимаемый 1 кг газа, может быть различен в зависимости от условий, при которых он находится. Для удобства сопоставления объемных расходов газа и других практических измерений вводят понятие нормальных условий. Условия, при которых рабочее вещество находится под давлением 101325 Па (760 мм рт. ст.) при температуре 273,15 K (0 ºC), называются нормальными. Единицу измерения объема газа при нормальных условиях обозначают нм³.

Законы идеального газа

Введенное ранее понятие идеального газа базируется на представлении о молекулах, образующих газ, как материальных точках, взаимодействие которых между собой ограничивается соударениями. Для идеального газа известно несколько законов, названных по имени их первооткрывателей. Эти законы впервые были сформулированы на основании опытов с реальными газами при давлениях, близких к атмосферному.

Так, закон Бойля-Мариотта (названный в честь двух ученых, независимо пришедших к одинаковому результату) устанавливает, что при неизменной температуре произведение давления газа на его объем постоянно:

рv = const. (1.6)

Если уравнение (1.6) записать для двух произвольных состояний, то получим р₁v₁ = р₂v₂, откуда

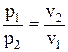, (1.7)

т. е. при постоянной температуре давление и объем изменяются обратно пропорционально.

Ж. Гей-Люссак установил, что при постоянном давлении объем газа с подводом тепла увеличивается пропорционально температуре по линейной зависимости:

V = V₀ (1 + a t), (1.8)

где V, V₀ – объем газа при t и 0 °C соответственно;

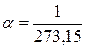– коэффициент объемного расширения газов, K ^–1.

Для температуры t₁ и t₂ отношение конечных объемов V₁ и V₂ получаем из уравнения (1.8), вынося за скобки a и произведя сокращение:

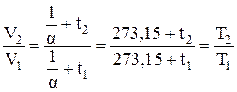. (1.9)

Если к газу подводить тепло при неизменном объеме, то закон Гей-Люссака записывается в виде

р = р₀ (1 + a t), (1.10)

а соотношение между давлением и температурой:

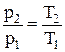. (1.11)

Законы Бойля-Мариотта и Гей-Люссака дают соотношение между какими-либо двумя различными параметрами из трех известных основных параметров: Т, р, v. Уравнение, связывающее все три параметра в виде

pv = RT, (1.12)

называется уравнением Клайперона. Оно однозначно связывает основные параметры состояния р, v и Т и является уравнением состояния идеального газа. Постоянная величина R зависит не от состояния газа, а от его свойств. Она называется газовой постоянной.

При высокой температуре и небольшом давлении уравнение (1.12) достаточно точно описывает состояние реальных газов. При низкой температуре и большом давлении, когда состояние газа близко к сжижению, применение этого уравнения дает весьма существенные расхождения с опытом, так как принятая модель идеального газа не подходит для сильно уплотненного реального газа.

Рассмотрим еще два закона идеальных газов. Пусть в двух одинаковых объемах заключены различные газы при равных давлении и температуре. Число молекул в первом объеме – N₁, масса каждой молекулы – m₁, во втором объеме соответственно – N₂ и m₂. Закон Авогадро утверждает: в равных объемах различных идеальных газов, находящихся при одинаковых температуре и давлении, содержится равное число молекул.

Из закона Авогадро вытекает два важных следствия.

1) Масса газа в первом объеме M₁ = N₁ m₁, масса газа во втором объеме M₂ = N₂ m₂ . Поскольку N₁ = N₂ , то отношение этих масс M₁ / M₂ = m₁ / m₂. Масса одной молекулы m чрезвычайно мала, поэтому для удобства расчетов вводят понятие моля газа. Молем m называют количество газа в килограммах, численно равное его молекулярной массе. Так, моль кислорода О₂ равен 32 кг/моль, окиси углерода СО – 28, водорода Н₂ – 2 и т. д. Из очевидной пропорции
m₁ / m₂ = m₁ / m₂ приходим к выводу о том, что массы различных идеальных газов, заключенных в равных объемах при одинаковых температуре и давлениии, относятся между собой как их молекулярные массы, т. е.

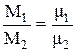. (1.13)

2) Равенство (1.13) перепишем в виде М₁ / m ₁ = М₂ / m ₂ , где отношение массы всего газа к его молекулярной массе есть число молей газа К = М / m. Мы приходим к выводу, что в равных объемах газов, находящихся при одинаковых давлениях и температурах, содержится равное число молей газов: К₁ = К₂. Выразим объем первого газа V₁ как произведение объема одного моля m₁v₁ на число молей К₁: V₁ = m₁v₁K₁. Для второго объема соответственно V₂ = m₂v₂K₂. Поскольку V₁ = V₂ , то m₁v₁ = m₂v₂ , объем моля для любых идеальных газов, находящихся при одинаковых температуре и давлении, есть величина постоянная:

mv = const. (1.14)

При нормальных условиях mv = 22,4 м³/моль. Это легко проверить на примере любого газа. Так, для кислорода m_О2 = 32 кг/моль, v_О2 = 0,7 м³/кг,
mv = 32×0,7 = 22,4 м³/моль.

Перейдем к определению величины газовой постоянной R. Уравнение состояния (1.12) для одного моля газа имеет вид:

pmv = mRT. (1.15)

Подставляя численные значения р, Т и mv для нормальных условий,
находим

,

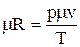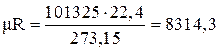Дж/(моль×K). (1.16)

Эта величина одинакова для всех газов и называется универсальной газовой постоянной. Значение газовой постоянной R зависит от молекулярной массы газа и определяется по формуле:

,

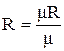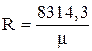Дж/(кг×K). (1.17)

Рассмотрим теперь идеальный газ, состоящий не из однородных молекул, а из молекул различных компонентов. Модель такого идеального газа будет представлять собой совокупность хаотически движущихся материальных точек, не имеющих объема, но масса и скорость этих материальных точек различны. Молекулы каждого компонента оказывают на стенки сосуда некоторое давление p_i, называемое парциальным, а общее давление, оказываемое на стенки сосуда молекулами всех n компонентов, равно сумме парциальных давлений каждого из компонентов:

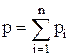. (1.18)

Это положение носит название закона Дальтона.

Смеси идеальных газов

Под газовыми смесями понимают механическую смесь нескольких газов, которые не находятся между собой в химическом взаимодействии. Каждый из компонентов ведет себя в смеси так, как если бы он один занимал весь объем. Если компоненты смеси представляют собой идеальные газы, то и вся смесь является идеальным газом, подчиняется всем законам идеального газа и описывается уравнением состояния идеального газа:

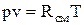, (1.19)

где R_см – газовая постоянная смеси.

Значение R_см может быть найдено по общей формуле:

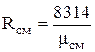, (1.20)

где m_см – средняя молекулярная масса газовой смеси.

Иногда m_см называют кажущейся молекулярной массой смеси, так как понятие моля для газовой смеси условно. Поскольку молекулярные массы компонентов m_i смеси различны, то m_см зависит от тех пропорций, в которых эта смесь составлена. Обычно состав смеси задается массовыми m_i или объемными r_i долями. Если смесь состоит из n компонентов и известны их массы M_i, то массовой долей является отношение:

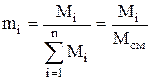. (1.21)

При этом очевидно, что 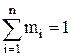. При объемном задании смеси каждый компонент (который в действительности занимает весь объем и находится под своим парциальным давлением) условно приводят к давлению смеси, под которым он занимает меньший объем, составляющий лишь некоторую часть объема смеси – так называемый приведенный объем V_i. Тогда по аналогии с уравнением (1.21) объемной долей является отношение приведенного объема компонента к объему смеси V_см:

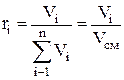. (1.22)

Сумма долей всех компонентов составляет единицу: .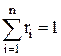

Связь между m_i и r_i может быть получена следующим образом:

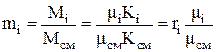. (1.23)

Так как 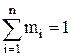, то 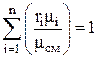. Отсюда кажущаяся молекулярная масса

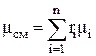. (1.24)

При массовом задании смеси

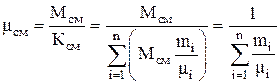. (1.25)

Таким образом, зная m _см и определив по выражению (1.20) R_см, можно для заданной смеси газов пользоваться уравнением состояния идеального газа (1.19). Для удобства расчетов в табл. 1.2 предлагается сводка формул для газовых смесей, где кроме полученных приводятся без вывода формулы для определения плотности смеси r_см и парциальных давлений р_i.

Таблица 1.2

Расчетные формулы для газовой смеси

Способ задания состава смеси	Параметр смеси
mсм,	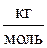Rсм,	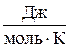rсм,	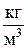рi, Па
В массовых долях		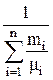8314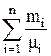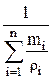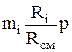
В объемных долях		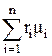		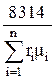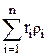ri p