Вопрос 24.2. Разностные методы дифференциальных уравнений. Метод Эйлера

Лишь немногие дифференциальные уравнения могут быть решены точно. На практике достаточно найти решение в некоторых заданных точках отрезка [a,b]. Так мы приходим к задаче численного решения дифференциального уравнения (задаче Коши).

Суть разностных методов состоит в том, что приближенное решение задачи Коши

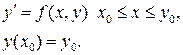
ищется на последовательности точек 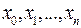и решение 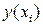в точке 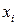приближается числом 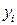, которое вычисляется по предыдущим значениям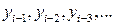

Если в разностном методе 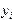вычисляется по k предыдущим значениям, то его называют k-шаговым. При 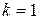получаем одношаговый метод. Все рассматриваемые ниже методы являются одношаговыми.

Совокупность точек 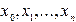называется сеткой, а сами ‑ узлами сетки. Разность между соседними узлами 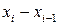называется шагом сетки. Если 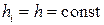, то есть узлы расположены на одинаковом расстоянии, то сетка называется равномерной, в противном случае неравномерной.

Примером простейшего одношагового разностного метода является метод Эйлера.

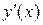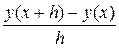Заменим на , тогда получим

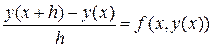
или

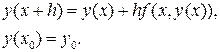
Пусть 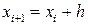, тогда положив, получим

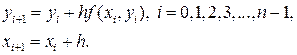
Полученные уравнения называются разностной схемой Эйлера. Подставляя сюда последовательно i=0,1,2,3,...n‑1 найдем сеточную функцию y, то есть решение разностной схемы Эйлера.

Методу Эйлера можно дать следующую геометрическую интерпретацию. Пусть y(x) есть решение задачи Коши. Построим его график (интегральную кривую) и из точки 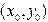проведем касательную, угловой наклон которой равен 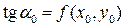. На этой касательной возьмем точку с абциссой 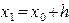, тогда очевидно ордината этой точки равна 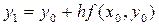. Продолжая этот процесс далее, получаем ломаную, называемую ломаной Эйлера. Ординаты вершин этой ломаной совпадают со значениями 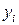, полученными из решения схемы Эйлера, абциссы вершин ломаной совпадают с узлами сетки (см. рис. 1).

Пусть теперь 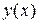есть функция, график которой является ломаной Эйлера, тогда можно доказать, что, если 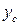есть решение задачи Коши, для которой выполнены условия

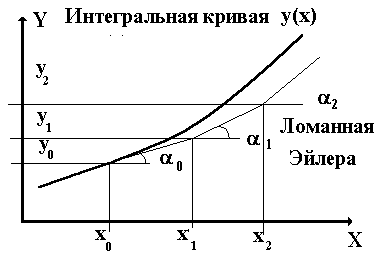
Рис 1. Ломаная Эйлера.

теоремы то существует константа C, такая что

.

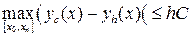Отсюда следует, что при h 0 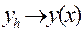, другими словами разностный метод Эйлера сходится к точному решению задачи Коши и имеет сходимость первого порядка. Таким образом, при уменьшении шага сетки в 2-а раза погрешность метода уменьшается в два раза.

На практике величина константы C, как правило, неизвестна. Тем неменее погрешность метода можно оценить по правилу Рунге

,

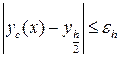где 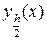, решение, полученное методом Эйлера с шагом в двое меньшим первоначального (x ‑ узел сетки с шагом h). Более того, решение можно уточнить по формуле Ричардсона

,

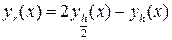которая имеет второй порядок сходимости.

Пример 24.2. Методом Эйлера найти численное решение задачи Коши и оценить его погрешность.

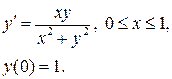
Схема Эйлера для данной задачи имеет вид

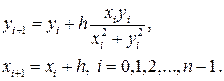
Выберем шаг h = 0.2. Результаты расчетов приведем в таблице

n	x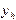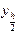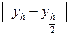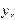
	0.0	1.0000	1.0000	0.0000	1.0000
	0.1		1.0000
	0.2	1.0000	1.0990	0.0990	1.1980
	0.3		1.1761
	0.4	1.1923	1.2395	0.0472	1.2867
	0.5		1.2923
	0.6	1.3015	1.3365	0.0350	1.3715
	0.7		1.3736
	0.8	1.3802	1.4045	0.0243	1.4288
	0.9		1.4301
	1.0	1.4339	1.4508	0.0169	1.4677

На рис. 2 представлены графики решения 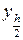и решения .

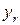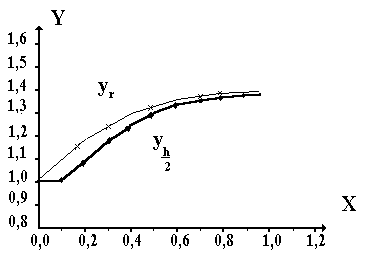
Рис. 2. Графики решени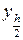й и 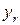задачи Коши.