Для схемы замещения, приведенной на рисунке 1.5, направленный граф электрической сети имеет следующий вид.

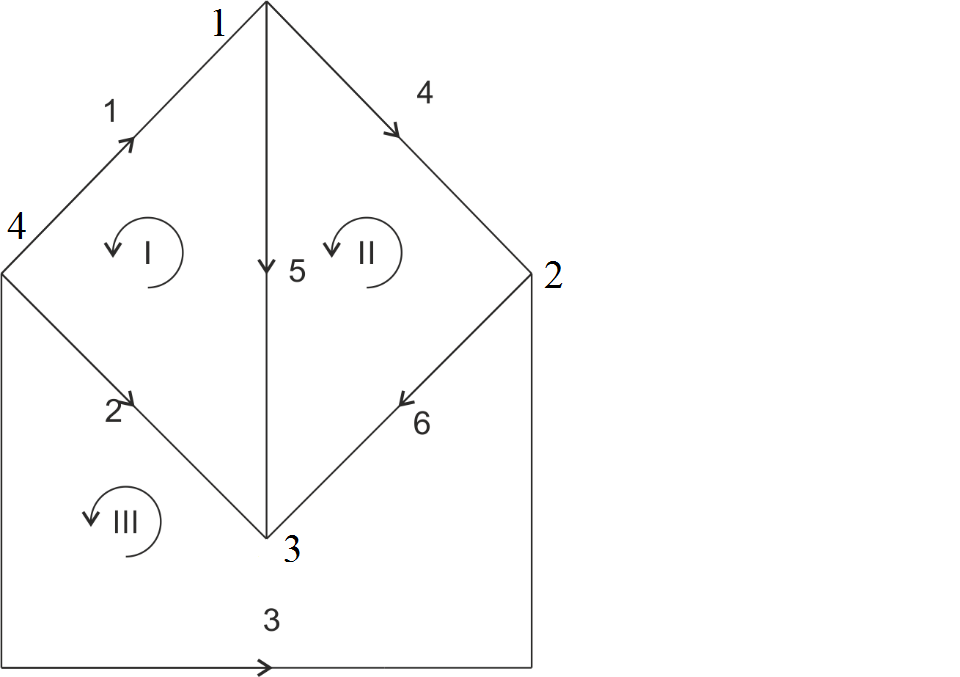
Рис.1.6 Направленный граф электрической цепи для схемы замещения, приведенной на Рис. 1.5

Направленный граф характеризует конфигурацию – геометрический образ схемы. Для аналитического представления графа должны быть пронумерованы узлы, ветви, независимые контуры и выбрано направление обходов этих контуров. В рассматриваемой схеме выбирается балансирующий узел.

Геометрию графа можно записать в алгебраической форме с помощью двух матриц соединений или инциденций.

1.5.2 Первая матрица соединений (инциденций) М или матрица соединений ветвей в узлах

Онапредставляет собой таблицу, строки которой отвечают узлам направленного графа электрической сети, а столбцы — ветвям.

Узлы без балансирующего (1.1)

М=

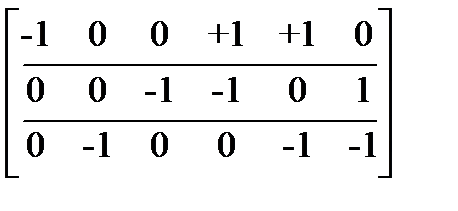
ветви

При составлении матрицы М балансирующий узел опускается.

Каждая строка матрицы М отвечает одному узлу, а каждый столбец – одной из ветвей. Элементы матрицы М могут принимать одно из 3-х значений:

+1 – если ветвь j выходит из узла i , т.е. узел i является началом ветви j;

m_ij = -1 – если ветвь j входит в узел i, т.е. узел i является концом ветви j;

0 – если ветвь j не связана с узлом i.

Первый закон Кирхгофа в матричной форме

Найдем произведение первой матрицы соединений М и столбцевой матрицы токов в ветвях.

Столбцевая матрица токов в ветвях

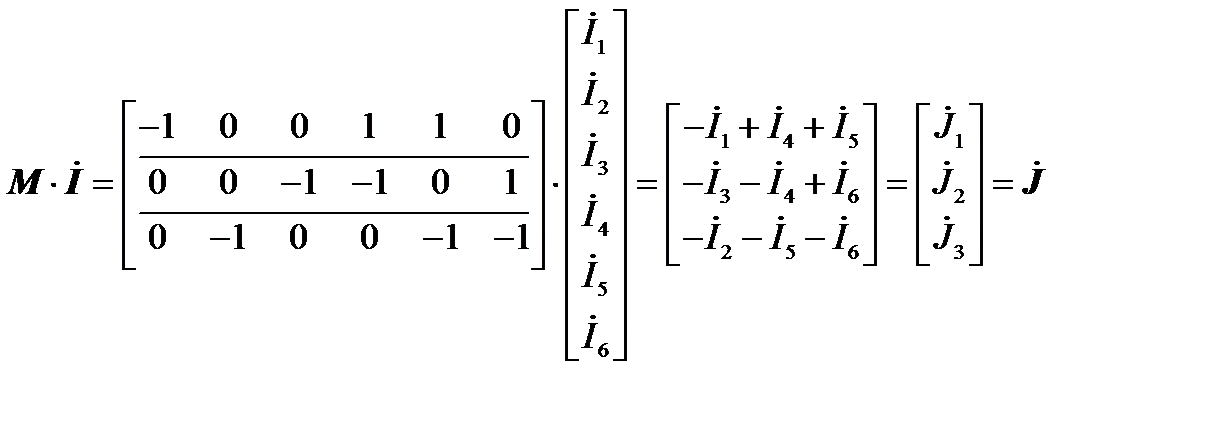
Столбцевая матрица задающих токов

Сопоставив алгебраические суммы токов в строках матрицы произведения, видим, что они равны задающим токам в соответствующих узлах (см. выражения в начале п. 1.5). Первый закон Кирхгофа в матричной форме формулируется так: произведение первой матрицы соединений и матрицы – столбца токов ветвей равно матрице – столбцу задающих токов.

Первый закон Кирхгофа в матричной компактной форме:

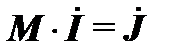. (1.2)

Матрица соединений (инциденций) ребра-пути Н.

Это матрица, строки которой соответствуют ребрам, а столбцы путям от корня графа (базисного узла) к узлам, где подключены нагрузки.

Элементы матрицы H — h_ij могут принимать два значения: 1— если ветвь i входит в путь j и 0 — если ветвь i не входит в путь j. Так, для разомкнутой сети, приведенной на Рис 1.7, матрица ребра – пути имеет вид

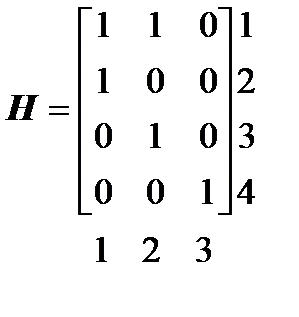ветви (ребра) (1.3)

пути

Пути от базисного узла к узлам с нагрузками

Пути	Соединения вершин	Ветви (ребра)
1- й путь	0-2	1,2
2 - й путь	0-3	1,3
3 - й путь	0-4

Матрицу H используют при определении в схеме токораспределения. По известным токам нагрузки в узлах можно рассчитать токи в ветвях, используя выражение

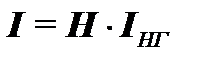(1.4)

Здесь 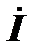— матрица-столбец токов ветвей.