Центр тяжести тела. Методы нахождения центра тяжести

На каждую частицу тела, находящегося вблизи поверхности Земли, действует направленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. 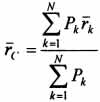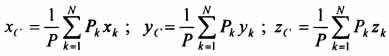Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно формулам и , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина 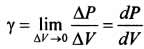называется удельным весом, а величина 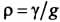- плотностью тела в данной точке. ("гамма"-Н/м3) ("ро"-Н*с2/м4)

Методы нахождения центра тяжести.

Метод симметрии.

Покажем, что если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или
в центре симметрии.

а. Пусть тело симметрично относительно плоскости Оху

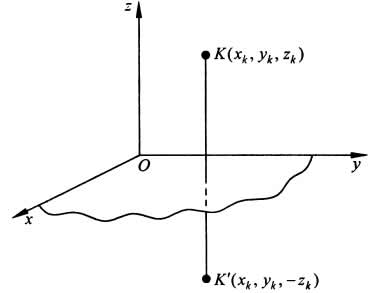
Тогда вследствие симметрии каждому элементу К тела объемом 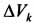( 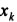, , 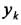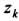) будет соответствовать элемент К' того же объема с координатами ( 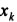, ,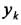- 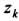). Поэтому статический момент объема 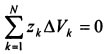и координата 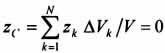. Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху.

б. Пусть тело симметрично относительно оси Oz.

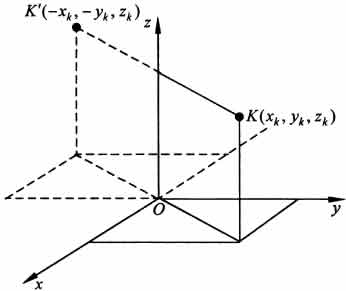
Тогда всякому элементу К тела объемом 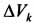с координатами ( 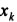, , 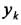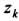) будет соответствовать такой же по объему элемент К', расположенный симметрично относительно оси Oz и имеющий координаты (- 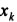,- , 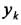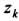). Поэтому статические моменты 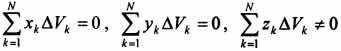и, следовательно, координаты 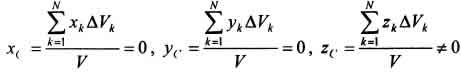. Таким образом, центр тяжести будет находится на оси симметрии.

в. Пусть тело имеет центр симметрии, который примем за начало координат. Тогда всякой частице тела объемом 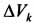, определяемой радиус-вектором rк, будет соответствовать частица такого же объема с радиус-вектором (-rк), симметричная ей относительно центра О. Поэтому 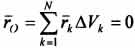. Следовательно, центр тяжести будет находиться в центре симметрии. Например, центры тяжести однородных куба, сферы, кольца, прямоугольной
или круглой пластины лежат в геометрическом центре этих тел.

Метод разбиения.

Этот метод основан на применении формул 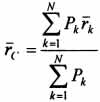и 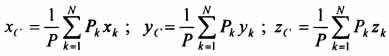. Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка.

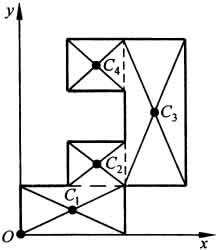
Расположив тело в системе координат, разделив его мысленно на отдельные части, веса которых Р1, Р2, Р3, Р4, а центры тяжести известны, вычислим вес тела и, согласно формулам 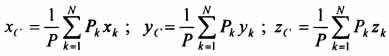, координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения).

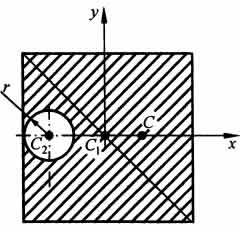
На рисунке изображена квадратная пластина, сторона которой а. В пластине выполнено круглое отверстие с радиусом r=0,2а и координатами центра x2=-0,3а; у2=0. Координаты центра тяжести С, пластины без отверстия x1=0, у1=0. Рассмотрим два тела: пластину без отверстия и диск, соответствующий вырезанному отверстию. При использовании формул 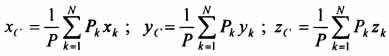вес диска будем считать отрицательным. Тогда 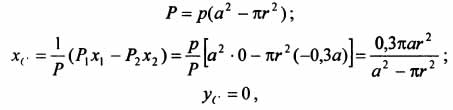, где р — вес единицы площади пластины.

Метод интегрирования.

Когда тело нельзя разбить на составные части, центры тяжести которых известны, используют метод интегрирования, являющийся универсальным.