Включение цепи r, C к источнику синусоидального напряжения.

Этот случай отличается от рассмотренного в п. 5.5. только тем, что источник представлен гармонической функцией, т.е., например,

Принужденное напряжение на емкости

а переходное напряжение на емкости

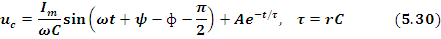
Если принять, что емкость не была заряжена, то постоянная интегрирования определяется при нулевых начальных условиях, т.е. u_c(0-). При t=0

Отсюда:

а для переходного напряжения на емкости получим

Кривая изменения напряжения изображена на рис. 5.10

Теперь перейдем к рассмотрению переходных процессов в электрической цепи, состоящей из последовательно соединенных r, L, C элементов. Здесь по аналогии с r, L и r, C цепями возможны случаи, когда цепь подключается к источнику постоянного напряжения или к источнику переменного напряжения, в частности, синусоидального напряжения, или цепь образует замкнутый контур без источников, но емкость к моменту коммутации была заряжена. Составленный по второму закону Кирхгофа дифференциальных уравнений для каждого из названных случаев имеет решение в форме (5.3), где первое слагаемое выражает принужденный режим, задаваемый видом функции в правой части, а второе выражает свободный режим в цепи при отсутствии внешних источников. Именно здесь и проявляется отличие рассматриваемой цепи, состоящее в том, что наличие в ней одновременно двух реактивностей разных знаков приводит к появлению квадратного характеристического уравнения и двух его корней p₁ и p₂. Теперь переходное напряжение на емкости равно

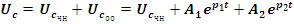
а ток в той же ветви

Две постоянные интегрирования A₁ и A₂ определяться из двух начальных условий в сочетании с двумя законами коммутации. Так, если непосредственно перед коммутацией заданы U_c(0-) и i_L(0-) т.е. начальные условия, то выполнение законов коммутации приводит к равенствам

где U_{c чн}(0+) и i_{c n0}(0+) - принужденные значения для момента времени непосредственно после коммутации. Когда они известны, так же как начальные условия U_{c чн}(0-) и i_{c n0}(0-) и корни p₁ и p₂ можно найти напряжения A₁ и A₂ и завершить решения (5.33) и (5.34). Проиллюстрируем все вышеизложенное на случае разряда емкости на цепь r , L (рис. 5.11).

Отсутствие источников питания означает, что в цепи для послекоммутационного периода t≥0 имеет место свободный режим и по второму закону Кирхгофа можно установить, что

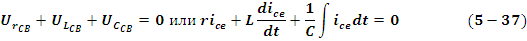
Т.к.

то при подстановке i_ce в равенство для U_{c чн} получим

Для решения этого дифференциального уравнения составим характеристической многочлен

Характер свободного режимам будет определяться видом корней этого уравнения, т.е. только параметрами цепи r, L, C. Так как эти корни определяться формулой

то характер свободного процесса зависит от знака подкоренного выражения.

Рассмотри возможных три случая.

Случай 1

Пусть d> ω₀, тогда согласно (5.40) корни характеристического уравнения p₁ и p₂ - отрицательные действительные числа, что делает свободный процесс обязательно затухающим.

Так как при разряде емкости принужденные напряжения и токи равны нулю, то полные их значения, как это следует из (5.33) и (5.34) будут равны свободным U_C=U_{C CB}, i=i_ce. Из начальных условий определяем значения постоянных интегрирования: при t<0, u_c (0-)=U₀ и i(0-)=0. Воспользовавшись равенством (5.35) и (5.36) получим

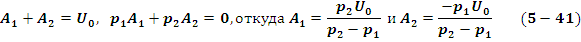
И окончательно

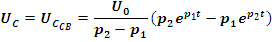
Кривые изменения напряжений на емкости и на индуктивности, тока и их составляющих приведены на рис. 5.12

Случай 2

Пусть d= ω₀, тогда корни характеристического уравнения станут одинаковыми p=p₁=p₂ и общее решение уравнения (5.38) дается в этом случае формулой

А для свободного тока

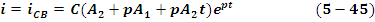
Подставляя значения A₁ и A₂ в формулы (5.44) и (5.45) найдем ток и напряжение на емкости

Определяем также напряжение на индуктивности

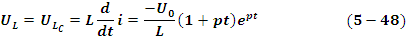
Кривые изменения i, U_L, U_CC по форме не отличаться от приведенных на рис 5.12

Случай 3

Если d< ω₀, то корни характеристического уравнения комплексные и сопряженные, а решение уравнения (5.38) при комплексных корнях его характеристического уравнения может быть записано в виде

где A и χ - постоянные интегрирования

так как начальные условия такие же как в двух предыдущих случаях, то по формулам (5.49) получим

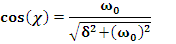
подставляя значения A, χ из (5.50) в уравнения (5.49) после некоторых преобразований получаем

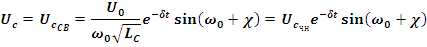
Где

Кривые изменений U_C, i показаны на рис. 5.13

· Основные понятия и определения. Операторный метод расчета

В электрических цепях могут происходить включения и выключения пассивных и активных ветвей, короткие замыкания отдельных участков, различного рода переключения, внезапное изменение параметров и т.д. Такие изменения, называемые коммутационными изменениями, являются причиной перехода цепи из одного установившегося состояния к другому. Если к источнику подключаться цепь, ни один участок которой не обладает сколько-нибудь заметной индуктивностью или емкостью, в цепи практически мгновенно устанавливаться тот режим, который был изучен в главе 2. Но если хоть один участок цепи обладает индуктивностью или емкостью, токи и напряжения во всех участках цепи достигают своих новых, установившихся, значений постепенно. Процесс перехода цепи из одного установившегося режима к другому, называется переходным процессом, а сопутствующие ему токи и напряжения на отдельных участках цепи - переходными напряжениями и токами. Причина этого явления заключается в том, что возникновение электрического поля в емкости и магнитного поля в индуктивности связано с накоплением в этих полях определенных количеств энергии, а это накопление не может происходить мгновенно. Так, накопление в электрическом поле конденсатора запаса энергии С u²/2 требует сообщения ему заряда q=Cu. Если конденсатор должен получить этот заряд в момент коммутации мгновенно, то ток в цепи i=C dU/dt,t=0 должен быть бесконечно велик и в цепи, всегда имеющей конечное сопротивление, не будет соблюдаться второй закон Кирхгофа. При накоплении запаса энергии L i²/2 в магнитном поле индуктивного участка цепи ток должен измениться от 0 до I. Если допустить, что в такой цепи в момент коммутации изменение тока происходит мгновенно, то напряжение на индуктивности Ldi/dt,t=0 будет равно бесконечности, и в цепи не будет соблюдаться второй закон Кирхгофа. Вышеуказанное позволяет сформулировать основные законы коммутации:

В любой ветви с индуктивностью ток в момент коммутации сохраняет то значение, которое он имел до коммутации, и дальше начнет изменяться именно с этого значения

В любой ветви напряжение на емкости сохраняет в момент коммутации то значение, которое оно имело до коммутации, и дальше начнет изменяться именно с этого значения

Здесь i_C(0-) и i_L(0-) - напряжение на емкости и ток на индуктивности в момент времени непосредственно перед коммутацией, i_C(0+) и i_L(0+) - соответственно в момент времени, непосредственно следующий за коммутацией.

Основой при расчете переходных процессов служат дифференциальные уравнения, составленные для конкретной электрической цепи в соответствии с законами Кирхгофа. Важно сразу отметить, что для линейных цепей с сосредоточенными параметрами, все уравнения являются линейными с постоянными коэффициентами. Примем, что коммутирующие устройства - ключи - являются идеальными.

Решение линейных дифференциальных уравнений при заданных с исчерпывающей полнотой начальных условиях часто удобно представлять в виде суммы двух функций (принцип суперпозиций):

из которых первая функция f₁(t) представляет собой частное решение заданного дифференциального уравнения, а вторая f₂(t) - общее, удовлетворяет однородному уравнению (правая часть равна нулю). Частное решение выражает принужденный режим, задаваемый источником. Если источник есть постоянная величина или периодическая функция времени, тогда такой режим будет одновременно и установившемся. Общее решение выражает поведение цепи при отсутствии внешних источников. Функции, определяющие общее решение, называют свободными составляющими. Все сказанное можно с учетом (5.3) отразить в общепринятой форме запаси, например, для переходного тока i=i_ce+i_пр напряжения u=u+u_пр и сразу подчеркнуть, что законом коммутации должно удовлетворять только полное решение.

Переходные процессы будем исследовать классическим методом, который заключается в интегрировании дифференциальных уравнений, связывающих токи и напряжения цепи. В результате интегрирования появляться постоянные, которые определяются из начальных условий. Начальными условиями называют значения действующих токов в индуктивностях и напряжений на емкостях, т.е. те величины, которые в момент коммутации (t=0) не изменяются скачком.

Начнем изучение переходных процессов с расчета простейших цепей, содержащих резисторы и только один реактивный элемент, т.е. индуктивность или емкость.

Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением.В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

Изображение заданной функции определяется в соответствии с прямым преобразованием Лапласа:

.

(1)

В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

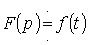или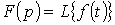

.

Следует отметить, что если оригинал увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.