Период решетки найдем из формулы условия максимума

, (2)

где j — угол, под которым наблюдается k-й максимум (рис. 4);

k — порядок (номер) максимума.

Ввиду того, что для максимума 1-го порядка угол мал, можно принять

, (3)

Подставив в формулу (2) выражение синуса угла из (3), определим постоянную решетки

, (4)

С учетом (4) формула (1) примет вид:

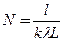, (5)

Рис. 4

Выпишем числовые значения, выразив их в СИ, и подставим в (5): l = 33 см = 3,3×10^{-2 м, L=110 см = 1,10 м, k=1,} l=600 нм = 600×10^{-9 м = 6}×10^{-7 м;}

.

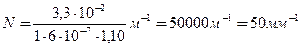Задача 11. Максимум энергии излучения абсолютно черного тела при некоторой температуре приходится на длину волны l₀=1 мкм. Вычислить излучательность (энергетическую светимость)* R_e тела при этой температуре и энергию W, излучаемую с площади S=300 см² поверхности тела за время t=1 мин Определить также массу, соответствующую этой энергии.

Решение: Излучательность абсолютно черного тела определяется по формуле закона Стефана — Больцмана:

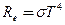, (1)

где s — постоянная Стефана — Больцмана, Т — абсолютная температура тела.

Абсолютную температуру определим из закона смещения Вина:

,

Откуда

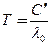, (2)

где l₀ — длина волны, на которую приходится максимум излучения при температуре Т; С' — постоянная Вина.

Подставив выражение для Т из (2) в (1), получим

. (3)

Выпишем числовые значения в СИ: s =5,67×10^-8 Вт/(м²×К⁴); С' = 2,89×10^{-3 м}×К, l_о=1 мкм=10^{-6 м.}

Проверим единиц» величин правой и левой частей формулы (3):

Вт/м² = Вт/(м²×К⁴)×(м×К/м)⁴, Вт/м² = Вт/м².

Вычислим

.

Энергию, излучаемую с площади S поверхности тела за 1 мин. определим по формуле

W = R_eSt. (4)

Выпишем числовые значения в СИ: R_e = 3,95×10⁶ Вт/м², S = 300 см² = 3×10^{-2 м2}, t =1 мин = 60 с.

Проверим единицы величин правой и левой частей формулы (4): Дж = Вт/м²×м²×с, Дж = Дж.

Вычислим W = 3,95×10⁶×3×10^-2×60 Дж=7,10×10⁶ = 7,10 МДж.

Массу т излучения определим, исходя из закона Эйнштейна взаимосвязи энергии и массы

Е = mс², (5)

где с — скорость света в вакууме, Е — энергия;

Откуда

. (6)

Выпишем числовые значения величин и вычислим массу;

E=W = 7,10×10⁶ Дж, с = 3×10⁸ м/с;

.

* Излучательность (энергетическая стоимость) – это величина, численно равная энергии, излучаемой в единицу времени с единицы площади тела.

Задачи для самостоятельного и индивидуального решения

Гармонические колебания

4.1.1. Точка совершает гармонические колебания, период колебаний 2 с, амплитуда колебаний 5 см, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 2,5 см.

4.1.2. Материальная точка массой 5 кг совершает гармонические колебания по закону 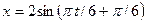см. Определить полную энергию колебаний, а также потенциальную и кинетическую энергию через две секунды после начала колебаний.

4.1.3. Материальная точка совершает гармонические колебания по закону 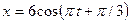см. Через какое время от начала движения смещение точки впервые достигнет значения 3 см?

4.1.4. Материальная точка совершает гармонические колебания по закону 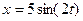см. Определить ускорение точки в момент времени, когда ее скорость равна 8 см/с.

4.1.5. Начальное смещение точки, что совершает гармонические колебания, равно 2 см, период колебаний 4 с, максимальное ускорение 5 см/с². Определить начальную фазу колебаний.

4.1.6. Точка совершает гармонические колебания по закону синуса. Амплитуда колебаний 4 см, энергия колебаний 2·10^-6 Дж. При каком смещении положения равновесия на точку действует сила 1,5·10^-5 Н?

4.1.7. Гармонические колебания величины s описываются уравнением , м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

4.1.8. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой А = 8 см, если за t = 1 мин совершается п = 120 колебаний и начальная фаза колебаний равна 45°.

4.1.9. Материальная точка совершает гармонические колебания с амплитудой А = 4 см и периодом Т = 2 с. Напишите уравнение движения точки, если ее движение начинается с положения х₀ = 2 см.

4.1.10. Точка совершает гармонические колебания с периодом Т = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

4.1.11. Точка совершает гармонические колебания по закону 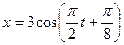, м. Определите: 1) период Т колебаний; 2)максимальную скорость υ_max точки; 3) максимальное ускорение а_max точки.

4.1.12. Точка совершает гармонические колебания с амплитудой А = 10 см и периодом Т = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

4.1.13. Скорость материальной точки, совершающей гармонические колебания, задается уравнением 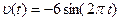, м/с. Запишите зависимость смещения этой точки от времени.

4.1.14. Написать уравнение гармонического колебания, амплитуда которого равна 10 см, период 10 с, начальная фаза равна нулю. Найти смещение и скорость колеблющегося тела через 1,25 с после начала колебаний.

4.1.15. Определите максимальное значение скорости и ускорения точки, совершающей гармонические колебания с амплитудой А = 3 см и периодом Т=4с.

4.1.16. Материальная точка, совершающая гармонические колебания с частотой v = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой x₀ = 5 см, со скоростью υ₀ = -15 см/с. Определите амплитуду колебаний.

4.1.17. Тело массой т = 10 г совершает гармонические колебания по закону , м. Определите максимальные значения: 1)возвращающей силы; 2) кинетической энергии.

4.1.18. Материальная точка массой т = 50 г совершает гармонические колебания согласно уравнению 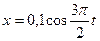, м. Определите: 1)возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

4.1.19. Материальная точка массой т = 20 г совершает гармонические колебания по закону , м. Определите полную энергию Е этой точки.

4.1.20. Тело массой 0,2 кг совершает гармонические колебания с циклической частотой 5 рад/с. Определите амплитуду колебаний, если полная энергия колебаний равна 0,1 Дж.

4.1.21. Полная энергия Е гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период Т колебаний равен 4 с, а начальная фаза .

4.1.22. Один математический маятник имеет период колебаний Т₁ = 3 с, второй Т₂ = 4 с. Каков период колебания математического маятника, длина которого равна суммедлин указанных маятников?

4.1.23. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А = 8 см. Определите жесткость к пружины, если известно, что максимальная кинетическая энергия Т_max груза составляет 0,8Дж.

4.1.24. Амплитуда гармонических колебаний равна 4 см, циклическая частота 10 с^-1, начальная фаза равна π/2. Написать уравнение колебаний. Найти максимальную скорость колеблющейся частицы.

4.1.25. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний груза возрастает в 2 раза. Определите массу первоначально подвешенного груза.

4.1.26. При подвешивании грузов массами т₁ = 600 г и т₂ = 400 г к свободным пружинам последние удлинились одинаково (l = 10 см). Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) каков из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз.

4.1.27. К стальной пружине подвешен некоторый груз, в следствии чего она удлинилась на 1 см. С каким периодом будет совершать этот груз гармонические колебания?

4.1.28. Пружинный маятник совершил за некоторое время 16 колебаний. Когда массу груза увеличили на 200 г, маятник совершил за то же время 15 колебаний. Какова была начальная масса груза?

4.1.29. Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определите период Т колебаний диска относительно этой оси.

4.1.30. Тонкий обруч радиусом R = 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определите период Т колебаний обруча.

4.1.31. Математический маятник, состоящий из нити длиной l = 1 м и свинцового шарика радиусом r= 2 см, совершает гармонические колебания с амплитудой А = 6 см. Определите: 1) скорость шарика при прохождении им положения равновесия; 2) максимальное значение возвращающей силы. Плотность свинца ρ= 11,3 г/см³.

4.1.32. Два математических маятника имеют одинаковую массу, длину, отличающиеся в п = 1,5 раза, и колеблются с одинаковой угловой амплитудой. Определите, какой маятник обладает большей энергией и во сколько раз.

4.1.33. Математический маятник длиной l = 1 м находится в кабине лифта. Определить период колебаний маятника, если лифт движется с ускорением а = 4,9 м/с: 1) вверх; 2) вниз.

4.1.34. Два математических маятника, длины которых отличаются на Δl = 16 см, совершают за одно и то же время один n₁ = 10 колебаний, другой - п₂ = 6 колебаний. Определите длины маятников l₁ и l ₂.

4.1.35. Математический маятник длиной l = 50 см подвешен в кабине самолета. Определите период Т колебаний маятника, если самолет движется: 1) равномерно; 2) горизонтально с ускорением а = 2,5 м/с².

4.1.36. Определите величину деформации пружинки под действием висящего на ней груза, если период малых колебаний груза равен 0,6 с. Ответ выразите в сантиметрах.

4.1.37. Математический маятник длиной l = 50 м подвешен в кабине самолета. Определить период колебаний маятника, если самолет движется с ускорением а = g под углом 30° к вертикали вниз, к Земле?

4.1.38. Гиря, подвешенная на пружине, совершает гармонические колебания с периодом 1 с. Скорость гири при прохождении положения равновесия равна 20 см/с. Найдите расстояние между крайними положениями гири.

4.1.39. Тело массой 10 г совершает гармонические колебания в горизонтальной плоскости под действием упругой силы со стороны пружины с коэффициентом жесткости 100 Н/м. Определите амплитуду колебаний, если максимальная скорость равна 3 м/с. Трением пренебрегите.

4.1.40. Два математических маятника начинают колебания с одинаковыми начальными фазами, но различными периодами 4 с и 5 с. Найдите максимальную частоту совпадения фаз колебаний.

4.1.41. Амплитуда гармонических колебаний материальной точки 2 см, полная энергия колебаний 0,3 мкДж. При каком смещении из положения равновесия на колеблющуюся точку действует сила 2,25·10^-5 Н?

4.1.42. Груз, свободно колеблющийся на пружине, за время 0,01 с сместился с расстояния 0,5 см от положения равновесия до наибольшего, равного 1 см. Каков период его колебаний?

4.1.43. Тело совершает гармонические колебания в горизонтальной плоскости на пружине жесткостью 300 Н/м. Амплитуда колебаний равна 4 см. Найдите полную энергию колебательного процесса.

4.1.44. Период гармонических колебаний тела возрастает с 1 до 2 с. Во сколько раз при этом уменьшается полная энергия колебаний, если амплитуда колебаний не меняется?

4.1.45. В колебательном контуре заряд одной из обкладок конденсатора меняется по закону , где Q - заряд в Кл, t - время в секундах. Найдите величину максимальной ЭДС самоиндукции в катушке индуктивности, если емкость конденсатора 0,5 мкФ.

4.1.46. Полная энергия колебаний в контуре равна 5 Дж. Найдите максимальную силу тока в контуре, если индуктивность катушки равна 0,1Гн.