Задача 1. Три группы продавцов продавали штучный товар, расфасованный в различные упаковки
Три группы продавцов продавали штучный товар, расфасованный в различные упаковки. После окончания срока распродажи был произведен тестовый контроль над случайно отобранными продавцами из каждой группы. Были получены следующие результаты:
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
Решение в пакете STATISTICA.
1. Запустить пакет STATISTICA.
2. Ввести исходные данные для переменных в столбцы VAR1 и VAR2 в следующем виде (нужно добавить 2 Cases: выполним команду Insert/Add Cases):
3. Выполнить команду Statistics/ANOVA. Появится меню General ANOVA/MANOVA (рис. 3.1).

Рис. 3.1.Меню General ANOVA/MANOVA
4. В нем выбрать пункт Analysis Wizard в колонке Specification Method. Нажать ОК.Откроется окно Variables (рис 3.2).
Определить независимую (VAR1) и зависимую (VAR2) переменные. Нажать ОК.

Рис. 3.2. Окно Variables
5. Появится панельANOVA Results.
6.Для решения данной задачи достаточно нажать кнопку All effects/Graphs, и в открывшемся окне поставить галочку возле SpreadSheet (рис.3.3). Нажать ОК:

Рис. 3.3.
7. В открывшемся окне появится результат решения задачи (рис. 3.4).

Рис. 3.4. Результат решения задачи
Итак, подчеркнутое предложение 1 –это ключ-решение: тут показан критерий Фишера-Снедекора, полученный в ходе решения задачи. Этот критерий надо сравнить с табличным  Фишера-Снедекора.
Фишера-Снедекора.
В столбце 2 показаны уровни фактора (1,2,3). Следующий столбец 3 показывает групповую среднюю для каждого уровня фактора (  ). А столбец 4 – показывает количество испытаний на каждом уровне фактора. Сравнив критерий Фишера-Снедекора полученный и табличный, делаем вывод о различии групповых переменных «в целом». Неотмеченные столбцы показывают различного рода погрешности расчетов, поэтому существенной роли не играют.
). А столбец 4 – показывает количество испытаний на каждом уровне фактора. Сравнив критерий Фишера-Снедекора полученный и табличный, делаем вывод о различии групповых переменных «в целом». Неотмеченные столбцы показывают различного рода погрешности расчетов, поэтому существенной роли не играют.
Варианты заданий
Вариант 1
1. Проведено по пять испытаний на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 12 испытаний, из них 5 – на первом уровне фактора, 4 – на втором и 3 – на третьем. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
Вариант 2
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
| 2.9 | 3.5 | 3.3 | |
| 3.7 | 3.1 | 3.3 | |
| 3.4 | 3.7 | 3.4 | |
| 3.1 | 3.0 | 3.2 |
2. Произведено 11 испытаний, из них 3 – на первом уровне фактора, 3 – на втором,
3 – на третьем и 2 – на четвертом. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | |||
| F1 | F2 | F3 | F4 | |
Вариант 3
1. Проведено по пять испытаний на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 12 испытаний, из них 4 – на первом уровне фактора, 5 – на втором,
3 – на третьем. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
| 2.8 | 2.9 | 3.7 | |
| 3.1 | 3.3 | 3.4 | |
| 3.6 | 3.0 | 3.7 | |
| 3.2 | 3.1 | ||
| 3.2 |
Вариант 4
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 13 испытаний, из них 3 – на первом уровне фактора, 2 – на втором, 4 – на третьем и 4 – на четвертом. Методом дисперсионного анализа при уровне значимости 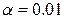 проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | |||
| F1 | F2 | F3 | F4 | |
| 83.5 | 91.5 | 82.5 | 91.5 | |
| 85.0 | 93.0 | 94.0 | 95.0 | |
| 87.0 | 83.5 | 90.5 | ||
| 85.5 | 89.0 |
Вариант 5
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания i | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 17 испытаний, из них 5 – на первом уровне фактора, 5 – на втором, 4 – на третьем и 3 – на четвертом. Методом дисперсионного анализа при уровне значимости 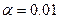 проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | |||
| F1 | F2 | F3 | F4 | |
Вариант 6
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 14 испытаний, из них 5 – на первом уровне фактора, 5 – на втором,
4 – на третьем. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
Вариант 7
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 15 испытаний, из них 4 – на первом уровне фактора, 3 – на втором, 4 – на третьем и 4 – на четвертом. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
| Номер испытания | Уровни фактора | |||
| F1 | F2 | F3 | F4 | |
| 25.7 | 25.01 | 25.9 | 24.6 | |
| 25.75 | 25.03 | 25.8 | 24.8 | |
| 25.8 | 25.05 | 25.75 | 25.0 | |
| 25.95 | 25.6 | 25.1 |
Вариант 8
1. Проведено по четыре испытания на каждом из трех уровней фактора. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| F1 | F2 | F3 | |
2. Произведено 14 испытаний, из них 4 – на первом уровне фактора, 3 – на втором, 3 – на третьем и 4 – на четвертом. Методом дисперсионного анализа при уровне значимости  проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
проверить гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями
