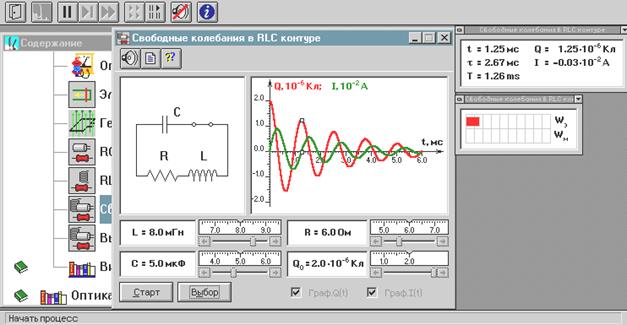
Свободные колебания в контуре

Ознакомьтесь с теорией в конспекте, учебнике (Савельев, т.2, §89, §90). Запустите программу «Эл-магн.Кванты». Выберите «Электричество и магнетизм» и «Свободные колебания в RLC контуре». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).

ЦЕЛЬ РАБОТЫ:

* Знакомство с компьютерной моделью процесса свободных затухающих колебаний в электрическом колебательном контуре.

* Экспериментальное исследование закономерностей свободных затухающих колебаний.

* Экспериментальное определение величины индуктивности контура.

КРАТКАЯ ТЕОРИЯ:

КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах.

НАПРЯЖЕНИЕ НА КОНДЕНСАТОРЕ .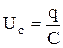

ЭДС самоиндукции в катушке .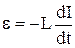

НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ .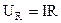

ОПРЕДЕЛЕНИЕ ТОКА .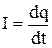

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных незатухающих колебаний

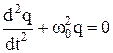, где w₀ = 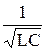- собственная частота контура .

Период Т = 2p .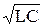

Его решение q(t) = q_v cos(w₀ t + a), где a - начальная фаза.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний

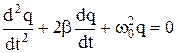, где b = 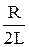- коэффициент затухания.

Его решение q(t) = q_v0 е^-bt cos(wt + a), где 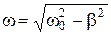- частота затухающих колебаний..

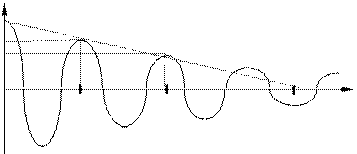
ПОСТОЯННАЯ ВРЕМЕНИ ЗАТУХАНИЯ в контуре t есть время, за которое амплитуда колебаний уменьшается в е = 2.73 раз. На графике зависимости амплитуды затухающих колебаний от времени касательная, проведенная к этому графику в начальный момент времени, пересекает ось времени в точке t = t.

q(t)

А₁

А₂ ---- касательная

А₃

t

t

t₂=Т t₃=2Т

ЛОГАРИФМИЧЕСКИМ ДЕКРЕМЕНТНОМ ЗАТУХАНИЯ называется величина, определяемая формулой 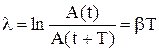. ДОБРОТНОСТЬ контура равна Q = .

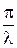МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ

Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.