Свойства степенного ряда и его суммы.

Почленное интегрирование или дифференцирование степенного ряда не меняют его радиус сходимости.

Доказательство. Под почленным интегрированием понимается интегрирование ряда 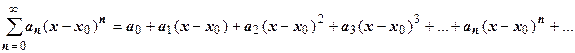по отрезку 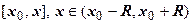. Результат этой операции: .

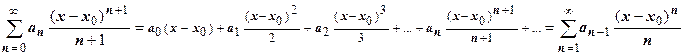Это тоже степенной ряд, его радиус сходимости 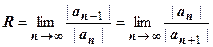равен радиусу сходимости исходного ряда.

Ряд, получающийся в результате почленного дифференцирования тоже степенной ряд: 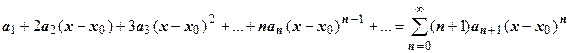. Его радиус сходимости 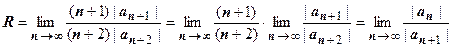тоже равен радиусу сходимости исходного ряда.

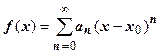2. (Почленное интегрирование степенного ряда).Пусть сумма степенного ряда на области сходимости равна функции , т.е. . Тогда для .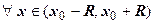

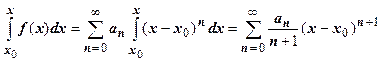Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда на отрезке иТеоремы 18.2.3.2 о почленном интегрировании равномерно сходящегося ряда.

3. (Почленное дифференцирование степенного ряда).Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и .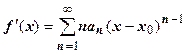

Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимости иТеоремы 18.2.3.3 о почленном дифференцировании равномерно сходящегося ряда.

4. (Бесконечная дифференцируемость суммы степенного ряда).Сумма степенного ряда в любой точке интервала сходимости имеет производные любого порядка; эти производные могут быть получены последовательным почленным дифференцированием исходного ряда.

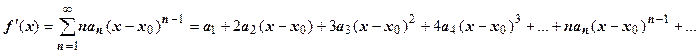
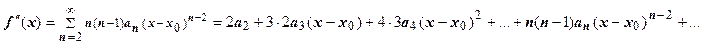
Доказательство. Справедливость этого утверждения следует из доказанной теоремы о почленном дифференцировании степенного ряда; последовательное применение этой теоремы даёт 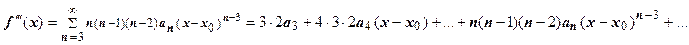и т.д.

18.2.5. Ряд Тейлора. Мы доказали, что сумма степенного ряда в любой точке интервала сходимости бесконечно дифференцируема. Выразим коэффициенты ряда через производные суммы (похожую задачу мы решали в разделе 7.7. Формула Тейлора).

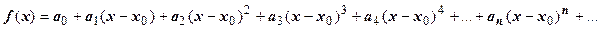. Положим здесь 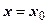. Все члены ряда, кроме нулевого, исчезают, и .

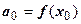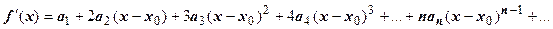. Положим 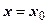, тогда .

. .

. .

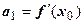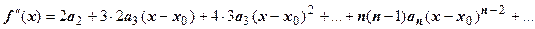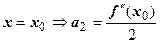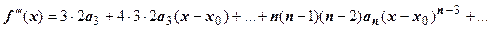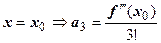Продолжая этот процесс, получим 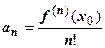. Заменив коэффициенты полученными выражениями, представим ряд как

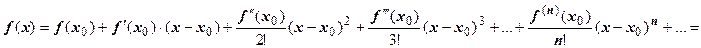
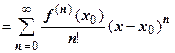. Ряд, стоящий в правой части этой формулы, называется рядом Тейлора функции . В частном случае, когда 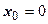и ряд принимает вид

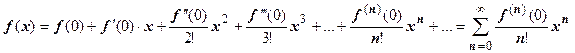, его принято называть рядом Маклорена. Напомним, что эти ряды получены в предположении, что - сумма степенного ряда и х - точка интервала сходимости.

Теперь рассмотрим обратную задачу: какой должна быть функция , чтобы её можно было представить в виде суммы степенного ряда? Первое, что очевидно, это то, что должна быть бесконечно дифференцируемой функцией (так как сумма ряда бесконечно дифференцируема). Второе - то, что коэффициенты ряда должны быть равны 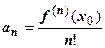. Поэтому предположим, что дана бесконечно дифференцируемая функция , мы нашли коэффициенты ряда по формуле 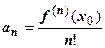, составили формальный ряд 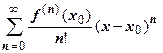и нашли область его сходимости. Будет ли сумма этого ряда на области сходимости равна ? Это тот вопрос, которым мы будем заниматься дальше.

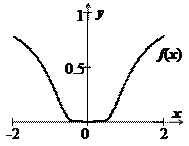
Приведём пример, когда ряд Маклорена функции сходится не к , а к другой функции. Пусть 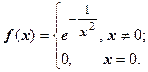Мы докажем, что все производные этой функции в точке х=0 равны нулю. При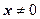 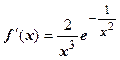. . 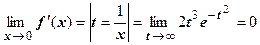Такие неопределённости придётся раскрывать при вычислении любой производной; заменой t=1/x они сводятся к неопределённостям, содержащим степенные и показательные функции, значение предела во всех случаях определяется пределом показательной функции и равно нулю. Значение производной в точке х=0 находим по определению производной:

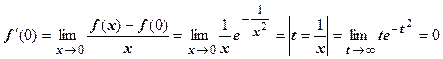. Итак, производная 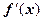непрерывна в точке х=0 и равна нулю. 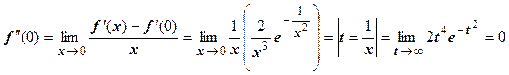и т.д. Так доказывается, что все производные в точке х=0 равны нулю. Как следствие, все коэффициенты ряда Тейлора этой функции равны нулю, и на всей числовой оси ряд сходится к функции, тождественно равной нулю, а не к .

Сформулируем условия, при которых ряд Тейлора функции сходится к этой функции. Эти условия удобно сформулировать в терминах остаточного члена формулы Тейлора. Напомним результаты раздела 7.7. Формула Тейлора: если имеет в окрестности точки 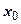все производные до n+1-го порядка включительно, то может быть представлена в виде формулы Тейлора с остаточным членом в форме Лагранжа: 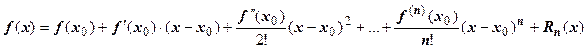, где 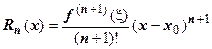- остаточный член в форме Лагранжа; 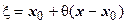- точка, расположенная между х и , .

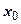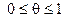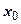Теорема.Для того, чтобы бесконечно дифференцируемая функция в окрестности точки разлагалась в ряд Тейлора, необходимо и достаточно, чтобы .

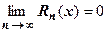Доказательство. Необходимость.Пусть в окрестности точки 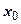функция представлена в виде сходящегося к этой функции ряда Тейлора 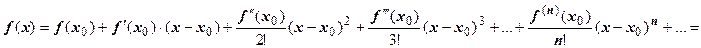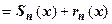, где 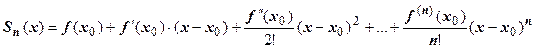- частичная сумма ряда, 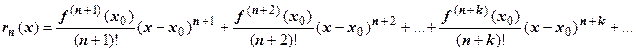- его остаток. Так как имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа: 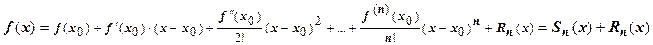. Сравнивая эти представления, получаем 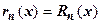. Из сходимости ряда к следует, что 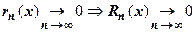, что и требовалось доказать.

Достаточность.Если 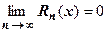, то 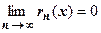, т.е. остаток ряда стремится к нулю при 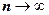, т.е. ряд сходится к функции .