Ортогональных координатах
При решении физических задач, обладающих той или иной симметрией, приходится пользоваться различными криволинейными ортогональными координатами. Краткое описание векторных соотношений и операторов теории поля в различных ортогональных координатах будет полезным как для усвоения теоретического материала, так и при выполнении предлагаемых заданий.
П1.1. Декартовы координаты
С декартовыми координатами x, y и z связана правая тройка единичных ортогональных векторов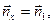 
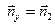и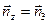 
. Элементы длины, площади и объема имеют вид:
,
.
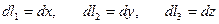
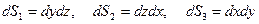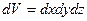Векторный оператор «набла» и оператор Лапласа записываются следующим образом
,
.
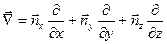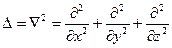При этом градиент скалярной функции j
,
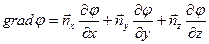дивергенция векторной функции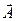 
,
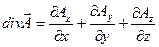и ротор векторной функции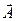
.
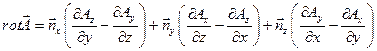