Необходимое условие экстремума
Рассмотрим функцию 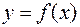 , определенную на промежутке
, определенную на промежутке 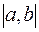 , и пусть точка
, и пусть точка 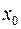 – внутренняя точка промежутка:
– внутренняя точка промежутка: 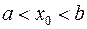 .
.
Определение 1. Точка 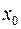 называется точкой (локального) максимума функции
называется точкой (локального) максимума функции 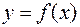 , если существует окрестность этой точки, в которой (при
, если существует окрестность этой точки, в которой (при 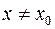 ) выполняется неравенство
) выполняется неравенство 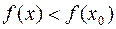 . Другими словами для малых приращений аргумента
. Другими словами для малых приращений аргумента 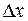 приращение функции
приращение функции 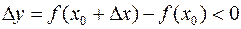 .
.
Определение 2. Точка 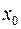 называется точкой (локального) минимума функции
называется точкой (локального) минимума функции 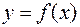 , если существует окрестность этой точки, в которой (при
, если существует окрестность этой точки, в которой (при 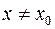 ) выполняется неравенство
) выполняется неравенство 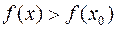 . Другими словами
. Другими словами 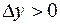 при малых
при малых 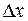 .
.
Точки максимума и минимума называются точками экстремума. Их можно характеризовать следующим образом: приращение функции в точке экстремума имеет постоянный знак, не зависящий от знака 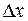 (если
(если 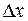 достаточно мало).
достаточно мало).
Теорема Ферма. Если функция 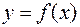 дифференцируема в точке
дифференцируема в точке 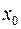 и имеет в этой точке локальный экстремум, то
и имеет в этой точке локальный экстремум, то 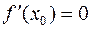 .
.
Доказательство. Дифференцируемость означает существование конечного предела
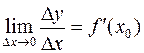 .
.
Для этого предела имеется три возможности: 1) 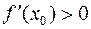 ; 2)
; 2) 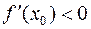 ;
;
3) 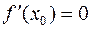 . Предположим, что
. Предположим, что 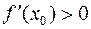 . Тогда для близких к нулю
. Тогда для близких к нулю 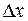 разностное отношение
разностное отношение 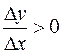 . Если же
. Если же 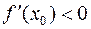 , то и
, то и 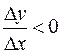 (для малых
(для малых 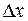 ). В обоих случаях знак
). В обоих случаях знак 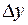 зависит от знака
зависит от знака 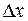 . Но по условию теоремы
. Но по условию теоремы 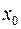 – это точка экстремума, значит, знак
– это точка экстремума, значит, знак 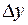 не зависит от знака
не зависит от знака 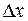 . Это противоречие означает, что
. Это противоречие означает, что 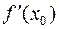 не может быть ни положительным, ни отрицательным. Остается последняя возможность:
не может быть ни положительным, ни отрицательным. Остается последняя возможность: 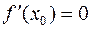 .
.
Замечание 1. Эта теорема имеет простой геометрический смысл: если в точке графика функции 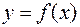 , которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная оси Ox.
, которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная оси Ox.
Замечание 2. Сформулированное в теореме условие 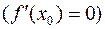 является необходимым, но не достаточным. Например, функция
является необходимым, но не достаточным. Например, функция 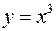 имеет производную
имеет производную 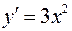 , которая обращается в ноль в точке
, которая обращается в ноль в точке 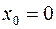 . Однако,
. Однако,
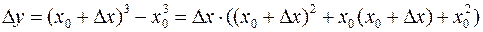 .
.
Выражение в скобках всегда положительно, как неполный квадрат суммы. Следовательно, 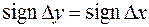 и в точке
и в точке 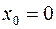 нет экстремума.
нет экстремума.
