Модуль 2 ­ Случайные селичины

Банк задач для подготовки к экзамену

ТГР ПГ 4 семестр

Математика.

Модуль 1. Случайные события.

1. В двух урнах содержатся белые и черные шары: в первой урне 5 белых и 7 черных, во второй урне 3 белых и 10 черных. Из каждой урны одновременно извлекли по одному шару. Найти вероятность того, что хотя бы один из вынутых шаров будет черным.

2. На склад поступают детали с заводов 1 и 2. 30 % деталей поступает с завода 2. Завод 1 выпускает 80 % отличных деталей, а завод 2 - 75 % отличных деталей. Подсчитать вероятность того, что наугад взятая со склада деталь не будет отличной.

3. В двух ящиках содержатся синие, черные и красные шары: в первом ящике 4 синих, 2 черных и 7 красных, во втором - 3 синих, 1 черный и 5 красных. Из каждого ящика извлекают по одному шару. Найти вероятность того, что хотя бы один из вынутых шаров будет красным.

4. Имеются 3 урны, в каждой из которых содержатся 7 белых и 4 черных шара, и 2 урны, в каждой их которых 5 белых и 1 черный шар. Какова вероятность вынуть белый шар из наугад выбранной урны, если предполагается, что выбор любой урны имеет одну и ту же вероятность.

5. Вероятность поражения стрелком мишени при одном выстреле равно 0,8. Найти вероятность того, что при четырех последовательных выстрелах будет не более 2 промахов.

6. Каждый из двух игроков бросает один раз игральную шестигранную кость. Найти вероятность того, что у первого игрока выпадет большее число очков.

7. Два стрелка стреляют в цель. Вероятность поражения цели при одном выстреле первым стрелком равна 0,8, вторым - 0,9. Найти вероятность того, что: а) оба стрелка поразят цель; б) хотя бы один стрелок поразит цель; в) только один стрелок попадет в цель; г) оба стрелка промахнутся.

8. Определить вероятность того, что при шестикратном бросании шестигранной игральной кости четное число очков выпадет не менее двух раз.

9. В тире имеются четыре ружья, вероятность попадания стрелком в цель для каждого из них соответственно равна 0,6; 0,7; 0,8; 0,9. Стрелок берет наугад ружье и дважды стреляет в цель. Какова вероятность поражения цели.

10. В ящике лежат 100 деталей, 20 из которых изготовлены одним заводом и 80 - другим. Первый завод изготавливает хороших деталей 90 %, а другой - 80 %. Определить вероятность того, что две наугад вынутые детали окажутся хорошими.

11. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,3. Опыт повторяют 100 раз. Найти вероятность того, что случайное событие А появится от 20 до 40 раз.

12. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,2. Опыт повторяют 500 раз. Найти вероятность того, что относительная частота появления события А отклонится от Р = 0,2 не более, чем на 0,1.

13. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,5. Сколько раз нужно провести опыт для того, чтобы с вероятностью большей, чем 0,9, можно было ожидать отклонение частоты появления события А от Р = 0,5 не более, чем на 0,1.

14. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,7. Опыт повторяют 1000 раз. Найти, какое отклонение относительной частоты появления события А от Р = 0,7 можно ожидать с вероятностью 0,8.

15. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,55. Опыт повторяют 400 раз. Какова вероятность того, что событие А появится в большинстве из проведенных опытов.

16. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью Р = 0,4. Опыт повторяют 850 раз. Какова вероятность того, что событие А появится в меньшинстве из проведенных опытов.

Модуль 2 ­ Случайные селичины

17. Дана дискретная случайная величина Х в виде таблицы, в первой строке указаны значения случайной величины, а во второй строке – вероятности, с которыми принимаются эти значения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение величины Х. Написать функцию распределения этой величины и построить график.

Х
Р	0,2	0,1	0,4	0,3

Х
Р	0,1	0,2	0,3	0,4

18. Задана непрерывная случайная величина Х своей функцией распределения F(x). Требуется:

1) Определить коэффициент А;

2) Найти плотность распределения вероятностей f(x);

3) Схематически построить графики F(x) и f(x);

4) Вычислить математическое ожидание и дисперсию Х;

5) Найти вероятность того, что Х примет значения из интервала (α, β).

19.

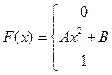
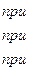
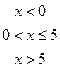
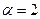
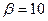
20.

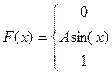
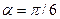
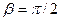
21.

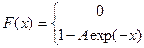
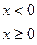
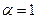
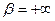
22.

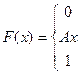
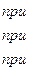
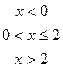
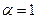
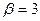
23.

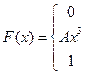
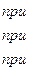
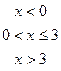
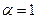
24. Задана непрерывная случайная величина X своей функцией плотности f(x). Требуется:

1) Определить коэффициент А;

2) Найти функцию распределения F(x);

3) Схематически построить графики F(x) и f(x);

4) Вычислить математическое ожидание и дисперсию Х;

5) Найти вероятность того, что Х примет значения из интервала (α, β).

A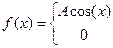

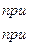
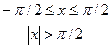
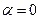
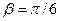
B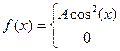

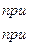
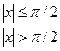
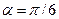
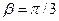
C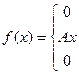

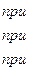
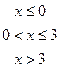
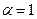
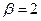
D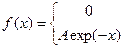

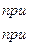
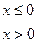
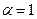
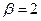
E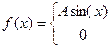

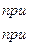
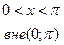
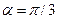
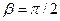
25. Задана нормально распределенная случайная величина X своими параметрами а (математическое ожидание) и σ (среднее квадратическое отклонение). Требуется:

1) Написать плотность вероятности f(x) и схематически изобразить ее график;

2) Найти вероятность того, что X примет значения из интервала (α, β);

3) Найти вероятность того, что X отклонится (по модулю) от а не более чем на δ.

A а = 10 σ = 1 α = 9 β = 12 δ = 2

B а = 11 σ = 2 α = 10 β = 13 δ = 2